In above question 1, find the speed of each speed of each particle, when the separation reduces to half its initial value
√Gmd
√2Gmd
√Gm2d
None of these
The correct Answer is:A
To solve the problem of finding the speed of each particle when the separation reduces to half its initial value, we can follow these steps:
1. Understanding the Initial Energy:
The gravitational potential energy (E_initial) between two particles of mass m separated by a distance d is given by:
Ei=−Gmmd
where G is the gravitational constant.
2. Final Separation:
When the separation reduces to half its initial value, the new distance becomes d2. The gravitational potential energy (E_final) at this new separation is:
Ef=−Gmmd2=−2Gmmd
3. Applying the Conservation of Energy:
The total mechanical energy is conserved. Therefore, the initial energy plus the kinetic energy of the particles must equal the final energy:
Ei+Ki=Ef+Kf
Assuming both particles start from rest, the initial kinetic energy Ki=0.
4. Setting Up the Equation:
The final kinetic energy when the separation is half can be expressed as:
Kf=12mv2+12mv′2
Since both particles are identical, we can denote their speeds as v and v′ (which will be equal). Thus:
Kf=mv2
5. Equating Energies:
Now we can set up the equation:
−Gmmd+0=−2Gmmd+mv2
Rearranging gives:
mv2=−Gmmd+2Gmmd
Simplifying:
mv2=Gmmd
6. Solving for Speed:
Dividing both sides by m:
v2=Gmd
Taking the square root:
v=√Gmd
Final Answer:
The speed of each particle when the separation reduces to half its initial value is:
v=√Gmd
The gravitational potential energy (E_initial) between two particles of mass m separated by a distance d is given by:
Ei=−Gmmd
where G is the gravitational constant.
When the separation reduces to half its initial value, the new distance becomes d2. The gravitational potential energy (E_final) at this new separation is:
Ef=−Gmmd2=−2Gmmd
The total mechanical energy is conserved. Therefore, the initial energy plus the kinetic energy of the particles must equal the final energy:
Ei+Ki=Ef+Kf
Assuming both particles start from rest, the initial kinetic energy Ki=0.
The final kinetic energy when the separation is half can be expressed as:
Kf=12mv2+12mv′2
Since both particles are identical, we can denote their speeds as v and v′ (which will be equal). Thus:
Kf=mv2
Now we can set up the equation:
−Gmmd+0=−2Gmmd+mv2
Rearranging gives:
mv2=−Gmmd+2Gmmd
Simplifying:
mv2=Gmmd
Dividing both sides by m:
v2=Gmd
Taking the square root:
v=√Gmd
The speed of each particle when the separation reduces to half its initial value is:
v=√Gmd
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.3
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
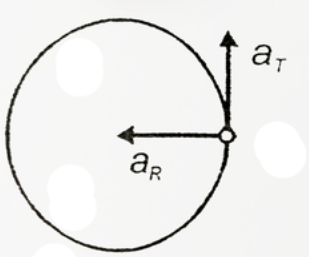
The time after which the speed of particle reduces to half of its initial value is
View SolutionTwo identical particles, each having a charge of 2.0×10−4C and mass of 10g, are kept at a separation of 10cm and then released. What would be the speeds of the particles when the separation becomes large?
View Solution
Knowledge Check
In the question number 38, the speed of the particle at this time is
A16 m s−1B26 m s−1C36 m s−1D46 m s−1In the question number 93, the time elapsed for its mechanical energy to drop half of its initial value is
A2.5 sB3.5 sC4.5 sD7.5 s
Two particles have equal masses of 5.0 g each and opposite charges of +4.0×10−5C. They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionIf the maximum speed of a particle on a travelling wave is v0, then find the speed of a particle when the displacement is half of the maximum value.
View SolutionA binary star system is revolving in a circular path with angular speed 'ω' and mass of the stars are 'm' and '4m' respectively. Both stars stop suddenly, then the speed of havirer star when the separation between the stars when the seperation between the stars becomes half of initial value is :
View SolutionTwo charged particle A and B repel each other by a force kr2 where is a constant and r is th separation between them. The particle A is clamped to a fixed point in the lab and the particle B which has a mass m, is released from rest with asn initial separartion r0 form A. Find the change in the potential energyof hte wo particle system as the separation increases to a large value. What will be the speed o the particle b in this situation?

View SolutionIf the speed of a particle moving at a relativistic speed is doubled, its linear momentum will
View SolutionA particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
View Solution
