Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
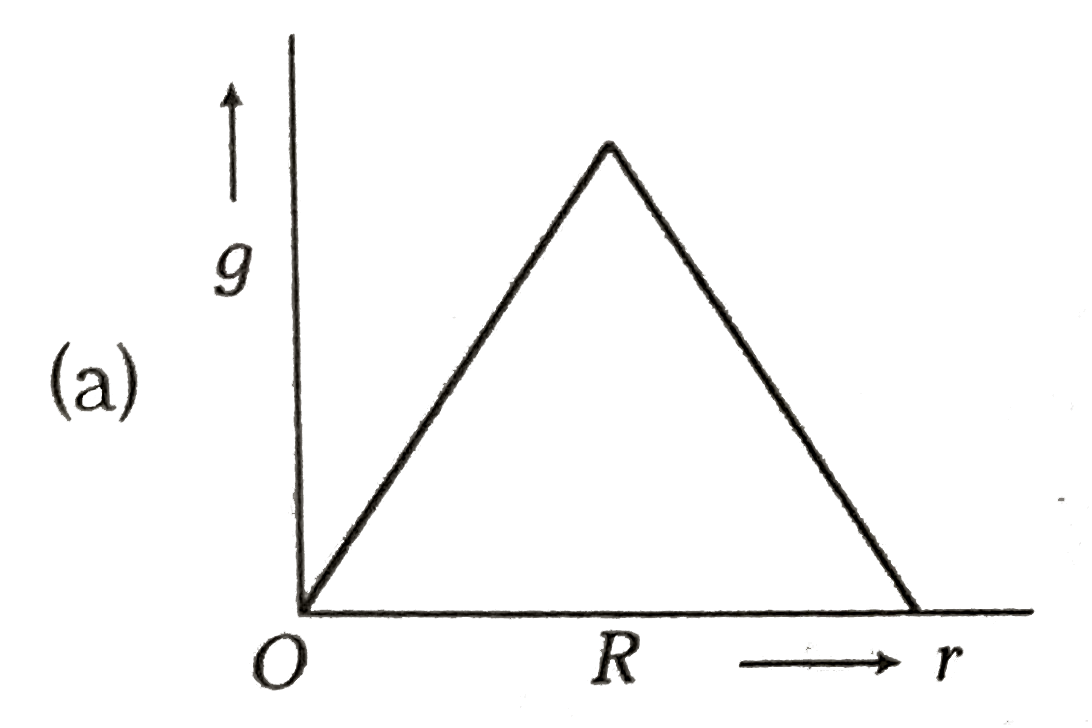
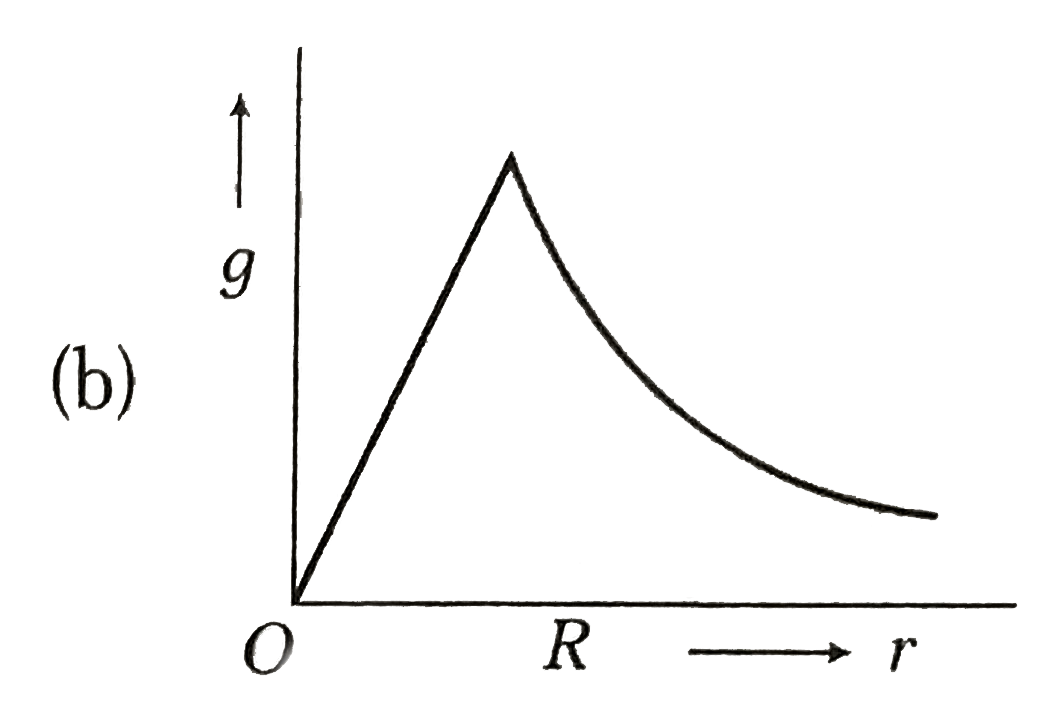
The correct Answer is:B
To solve the problem of how the acceleration due to gravity (g) varies from the center of the Earth to its surface, we can follow these steps:
Step 1: Understanding the formula for gravity inside the Earth
The acceleration due to gravity at a depth d below the surface of the Earth is given by the formula:
gdepth=gsurface(1−dR)
where:
- gdepth is the acceleration due to gravity at depth d,
- gsurface is the acceleration due to gravity at the surface of the Earth,
- R is the radius of the Earth.
Step 2: Analyzing the formula
From the formula, we can see that as d increases (moving deeper into the Earth), the term dR increases, which means gdepth decreases linearly. At the center of the Earth (where d=R), gdepth becomes zero.
Step 3: Behavior of gravity above the Earth's surface
For heights above the Earth's surface, the formula for gravity is:
gheight=gsurfaceR2(R+h)2
where h is the height above the surface. As h increases, gheight decreases.
Step 4: Graphical representation
1. From the center of the Earth to the surface (depth d), g starts from 0 and increases linearly to gsurface.
2. From the surface to a height h, g decreases as h increases.
Conclusion
The variation of g can be visualized as a linear increase from 0 at the center to gsurface at the surface, followed by a decrease as we move above the surface. Therefore, the correct graph representing this variation is option B.
The acceleration due to gravity at a depth d below the surface of the Earth is given by the formula:
gdepth=gsurface(1−dR)
where:
- gdepth is the acceleration due to gravity at depth d,
- gsurface is the acceleration due to gravity at the surface of the Earth,
- R is the radius of the Earth.
From the formula, we can see that as d increases (moving deeper into the Earth), the term dR increases, which means gdepth decreases linearly. At the center of the Earth (where d=R), gdepth becomes zero.
For heights above the Earth's surface, the formula for gravity is:
gheight=gsurfaceR2(R+h)2
where h is the height above the surface. As h increases, gheight decreases.
1. From the center of the Earth to the surface (depth d), g starts from 0 and increases linearly to gsurface.
2. From the surface to a height h, g decreases as h increases.
The variation of g can be visualized as a linear increase from 0 at the center to gsurface at the surface, followed by a decrease as we move above the surface. Therefore, the correct graph representing this variation is option B.
Topper's Solved these Questions
Similar Questions
If g is acceleration due to gravity on the surface of the earth, having radius R, the height at which the acceleration due to gravity reduces to g/2 is
View SolutionOne goes from the centre of the earth to a distance two third the radius of the earth. The acceleration due to gravity is highest at
View SolutionDoes the concentration of the earth's mass near its centre change the variation of g (acceleration due to gravity) with height from its surface?
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View SolutionThe ratio of the radius of the earth to that of the motion is 10. the ratio of the acceleration due to gravity on the earth to that on the moon is 6. The ratio of the escape velocity from the earth's surface to that from the moon is
View SolutionIf radius of earth shrinks by 1% then for acceleration due to gravity :
View SolutionThe value of acceleration due to gravity at the surface of earth
View SolutionIf the density of the planet is double that of the earth and the radius 1.5 times that of the earth, the acceleration due to gravity on the planet is
View SolutionA satellite of mass m is moving in a circular or orbit of radius R around the earth. The radius of the earth is r and the acceleration due to gravity at the surface of the earth is g. Obtain expressions for the following :
(a) The acceleration due to gravity at a distance R from the centre of the earth
(b) The linear speed of the satellite
(c ) The time period of the satelliteView SolutionAn artificial satellite is moving in circular orbit around the earth with speed equal to half the magnitude of escape velocity from the surface of earth. R is the radius of earth and g is acceleration due to gravity at the surface of earth (R=6400km)
Then the distance of satelite from the surface of earth is .View Solution

