A satellite of mass m is circulating around the earth with constant angular velocity. If the radius is R0 and mass of earth is M, then the angular momentum about the centre of the earth is
m√GM/R0
M√GmR0
m√GMR0
M√GM/R0
The correct Answer is:C
To find the angular momentum of a satellite of mass m revolving around the Earth with a radius R0 and mass M, we can follow these steps:
Step 1: Understand the formula for angular momentum
The angular momentum L of an object moving in a circular path is given by the formula:
L=m⋅v⋅r
where m is the mass of the object, v is the tangential (orbital) velocity, and r is the radius of the circular path.
Step 2: Determine the orbital velocity
For a satellite in circular orbit, the gravitational force provides the necessary centripetal force. The gravitational force acting on the satellite is given by:
F=GMmR20
where G is the gravitational constant. The centripetal force required to keep the satellite in circular motion is:
F=mv2R0
Setting these two forces equal gives:
GMmR20=mv2R0
We can cancel m from both sides (assuming m≠0):
GMR20=v2R0
Multiplying both sides by R0 gives:
GMR0=v2
Taking the square root of both sides, we find the orbital velocity v:
v=√GMR0
Step 3: Substitute the orbital velocity into the angular momentum formula
Now we can substitute v back into the angular momentum formula:
L=m⋅v⋅R0
Substituting for v:
L=m⋅(√GMR0)⋅R0
This simplifies to:
L=m⋅R0⋅√GMR0
Rearranging gives:
L=m⋅√GMR0
Final Answer
Thus, the angular momentum of the satellite about the center of the Earth is:
L=m√GMR0
---
The angular momentum L of an object moving in a circular path is given by the formula:
L=m⋅v⋅r
where m is the mass of the object, v is the tangential (orbital) velocity, and r is the radius of the circular path.
For a satellite in circular orbit, the gravitational force provides the necessary centripetal force. The gravitational force acting on the satellite is given by:
F=GMmR20
where G is the gravitational constant. The centripetal force required to keep the satellite in circular motion is:
F=mv2R0
Setting these two forces equal gives:
GMmR20=mv2R0
We can cancel m from both sides (assuming m≠0):
GMR20=v2R0
Multiplying both sides by R0 gives:
GMR0=v2
Taking the square root of both sides, we find the orbital velocity v:
v=√GMR0
Now we can substitute v back into the angular momentum formula:
L=m⋅v⋅R0
Substituting for v:
L=m⋅(√GMR0)⋅R0
This simplifies to:
L=m⋅R0⋅√GMR0
Rearranging gives:
L=m⋅√GMR0
Thus, the angular momentum of the satellite about the center of the Earth is:
L=m√GMR0
Topper's Solved these Questions
Similar Questions
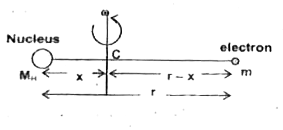
The angular momentum of the atom about the centre of mass will be
View SolutionA satellite of mass m moves along an elliptical path arouned the earth. The areal velocity of the satellite is proportional to
View SolutionA satellite of mass m moving around the earth of mass m in a circular orbit of radius R has angular momentum L. The rate of the area swept by the line joining the centre of the earth and satellite is
View SolutionA satellite of mass m orbits around the Earth of mas M in an elliptical orbit of semi - major and semi - minor axes 2a and a respectively. The angular momentum of the satellite about the centre of the Earth is
View SolutionA satellite of mass m goes round the earth along a circular path of radius r. Let mE be the mass of the earth and RE its radius then the linear speed of the satellite depends on.
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View Solutionif the earth is treated as a sphere of radius R and mass M, Its angular momentum about the axis of its rotation with period T, is
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View Solution
