Calculate moment of inertia w.r.t. rotational axis XX' in following figures.
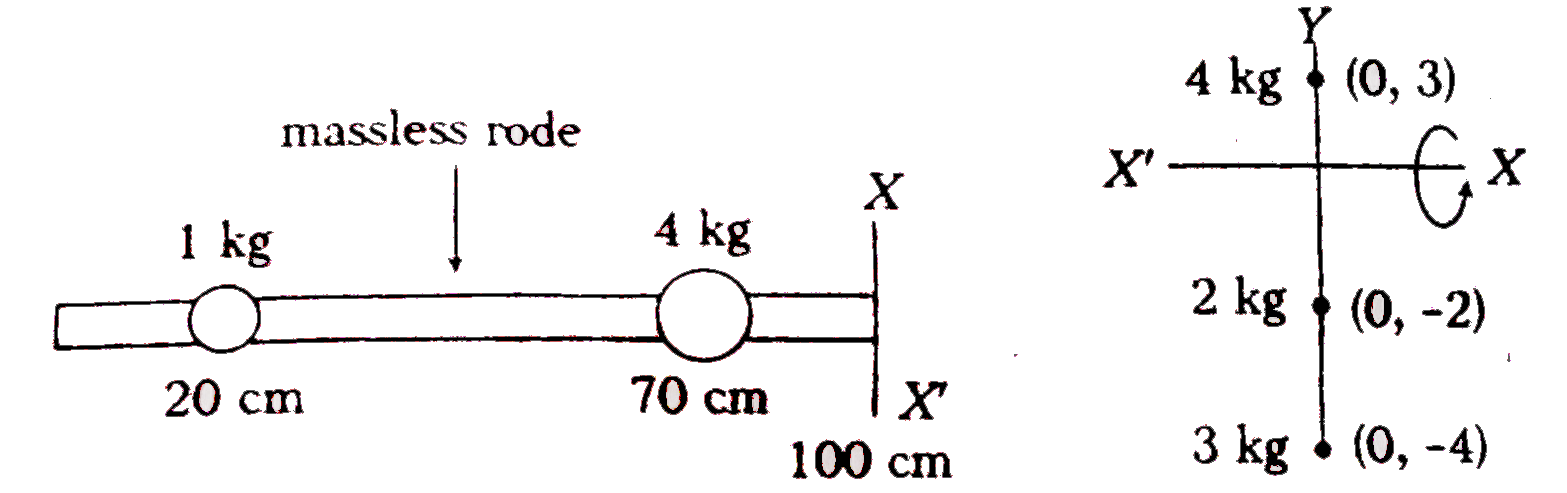
(i) Moment of inertia about XX'
IXX'=m1r21+m2r22=4×(1−0.7)2+1×(1−0.2)2
IXX'=4×(0.3)2+1×(0.8)2=1kg-m2
(ii) Moment of inertia about axis XX'
IXX'=4×(3)2+2×(2)2+3×(4)2=92kg-m2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.120videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.220videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
Similar Questions
The moment of inertia in rotational motion is equivalent to :
View SolutionCalculate the moment of inertia of the given rod about an axis CD
 View Solution
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.View SolutionCalculate the moment of inertia of the given rod about an axis CD.
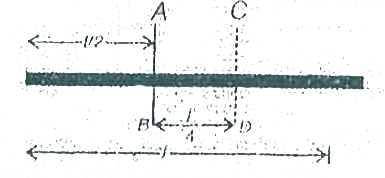 View Solution
View SolutionSurface mass density of disc of mass m and radius R is Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionCalculate the moment of inertia of
a. a ring of mass M and radius R about an axis coinciding with the diameter of the ring.
b. as thin disc about an axis coinciding with the diameter.View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be
 View Solution
View SolutionCalculate the moment of inertia of each particle in Fig. about the indicated axis of rotation.
 View Solution
View Solution
Calculate the moments of inertia of the figures shown, each having mass M, radius R and having uniform mass distribution about an axis perpendicular to the plane and passing through the centre?View Solution

