The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
L2√3
L212
L√3
L√2
The correct Answer is:A
To find the radius of gyration of a uniform rod of length L about an axis passing through its center of mass, we can follow these steps:
Step 1: Understand the Moment of Inertia
The moment of inertia I of a uniform rod of length L about an axis passing through its center of mass is given by the formula:
I=112ML2
where M is the mass of the rod.
Step 2: Relate Moment of Inertia to Radius of Gyration
The moment of inertia can also be expressed in terms of the radius of gyration k:
I=Mk2
where k is the radius of gyration.
Step 3: Set the Two Expressions for Moment of Inertia Equal
Since both expressions represent the moment of inertia, we can set them equal to each other:
112ML2=Mk2
Step 4: Cancel Mass M
Assuming M is not zero, we can cancel M from both sides:
112L2=k2
Step 5: Solve for Radius of Gyration k
Now, we can solve for k by taking the square root of both sides:
k=√112L2
This simplifies to:
k=L√12
Step 6: Simplify Further
We can simplify √12 as follows:
√12=√4×3=√4⋅√3=2√3
Thus, we can rewrite k:
k=L2√3
Final Answer
The radius of gyration of the uniform rod about an axis passing through its center of mass is:
k=L2√3
The moment of inertia I of a uniform rod of length L about an axis passing through its center of mass is given by the formula:
I=112ML2
where M is the mass of the rod.
The moment of inertia can also be expressed in terms of the radius of gyration k:
I=Mk2
where k is the radius of gyration.
Since both expressions represent the moment of inertia, we can set them equal to each other:
112ML2=Mk2
Assuming M is not zero, we can cancel M from both sides:
112L2=k2
Now, we can solve for k by taking the square root of both sides:
k=√112L2
This simplifies to:
k=L√12
We can simplify √12 as follows:
√12=√4×3=√4⋅√3=2√3
Thus, we can rewrite k:
k=L2√3
The radius of gyration of the uniform rod about an axis passing through its center of mass is:
k=L2√3
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
The radius of gyration of a uniform rod of length l , about an axis passing through a point l8away form the centre of the rod , and perpendicular to it is:
View SolutionThe radius of gyration of a uniform rod of length l , about an axis passing through a point l8away form the centre of the rod , and perpendicular to it is:
View Solution
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
Ak2+R2R2Bk2R2Ck2k2+R2DR2k2+R2
find the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
View SolutionThe mass of a unifprm rod is 0.4 kg and its length is 2 m. .Calculate the radius of gyration of the rod about an axis passing through its centre of mass and perpendicular to its length ?
View SolutionThe radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its centre will be
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is
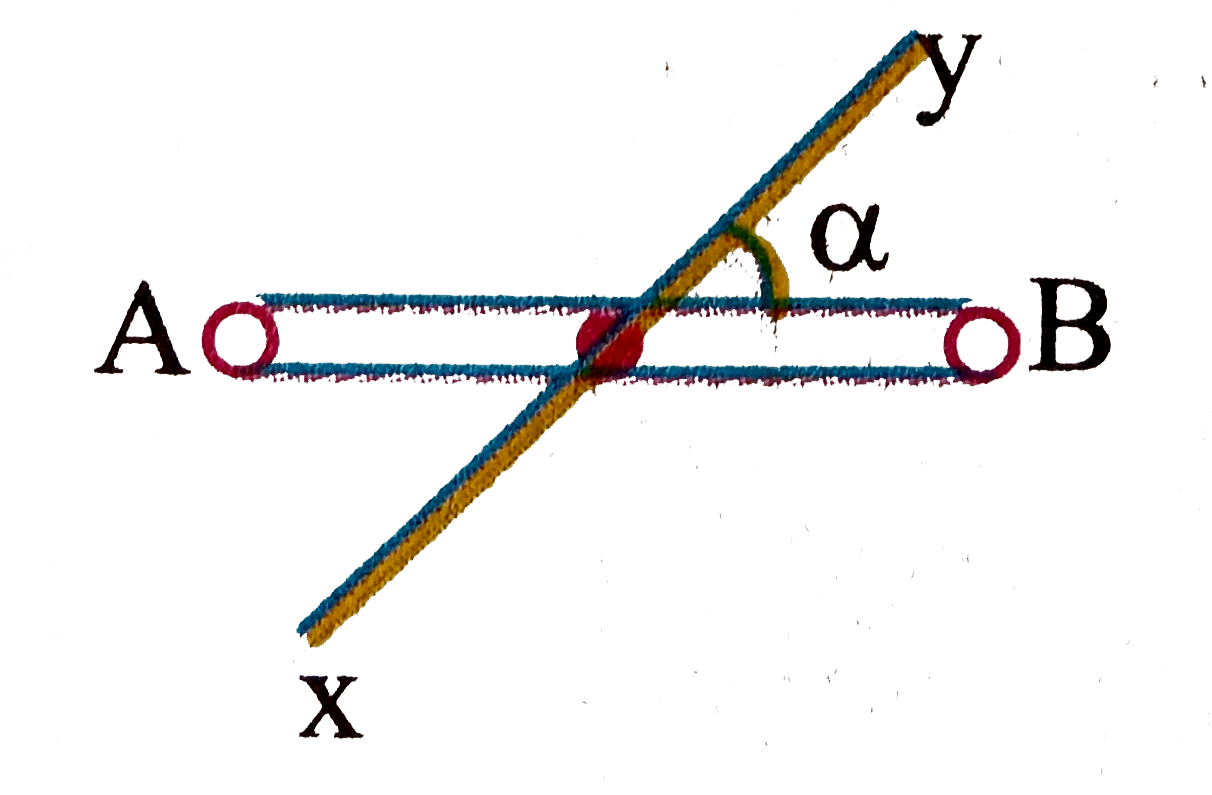
View Solution
