A rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
(mw+mb)L2/12
(mw+mb)L2/6
(mw+mb)L2/3
(mw+mb)L2/2
The correct Answer is:A
To find the moment of inertia I of a rod composed of two different materials (wood and brass) about an axis perpendicular to the rod and through its center, we can follow these steps:
Step 1: Understand the Structure of the Rod
The rod has a total length L and is composed of two equal halves:
- The first half (length L2) is made of wood with mass mw.
- The second half (length L2) is made of brass with mass mb.
Step 2: Moment of Inertia Formula for a Rod
For a uniform rod of length L and mass M, the moment of inertia I about an axis passing through its center and perpendicular to its length is given by the formula:
I=112ML2
Step 3: Calculate the Moment of Inertia for Each Material
Since we have two sections of the rod, we need to calculate the moment of inertia for both the wood and the brass sections:
1. For the wooden section (length L2):
- Mass mw
- Moment of inertia about its own center:
Iwood=112mw(L2)2=112mwL24=mwL248
2. For the brass section (length L2):
- Mass mb
- Moment of inertia about its own center:
Ibrass=112mb(L2)2=112mbL24=mbL248
Step 4: Combine the Moments of Inertia
Since the axis of rotation is through the center of the rod, we can simply add the moments of inertia of both sections:
I=Iwood+Ibrass=mwL248+mbL248=(mw+mb)L248
Step 5: Final Expression for Moment of Inertia
Thus, the moment of inertia I of the entire rod about the specified axis is:
I=(mw+mb)L248
Conclusion
The moment of inertia I of the rod about an axis perpendicular to the rod and through its center is:
I=(mw+mb)L212
The rod has a total length L and is composed of two equal halves:
- The first half (length L2) is made of wood with mass mw.
- The second half (length L2) is made of brass with mass mb.
For a uniform rod of length L and mass M, the moment of inertia I about an axis passing through its center and perpendicular to its length is given by the formula:
I=112ML2
Since we have two sections of the rod, we need to calculate the moment of inertia for both the wood and the brass sections:
- Mass mw
- Moment of inertia about its own center:
Iwood=112mw(L2)2=112mwL24=mwL248
- Mass mb
- Moment of inertia about its own center:
Ibrass=112mb(L2)2=112mbL24=mbL248
Since the axis of rotation is through the center of the rod, we can simply add the moments of inertia of both sections:
I=Iwood+Ibrass=mwL248+mbL248=(mw+mb)L248
Thus, the moment of inertia I of the entire rod about the specified axis is:
I=(mw+mb)L248
The moment of inertia I of the rod about an axis perpendicular to the rod and through its center is:
I=(mw+mb)L212
Topper's Solved these Questions
Similar Questions
A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
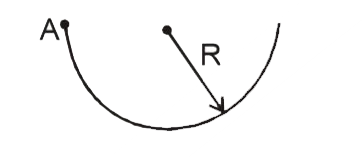 View Solution
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
 View Solution
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionA non-uniform rod AB has a mass M ad length 2l. The mass per unit length of the rod is mx at a point of the rod distant x from A. find the moment of inertia of this rod about an axis perpendicular to the rod (a) through A (b) through the mid-point of AB.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
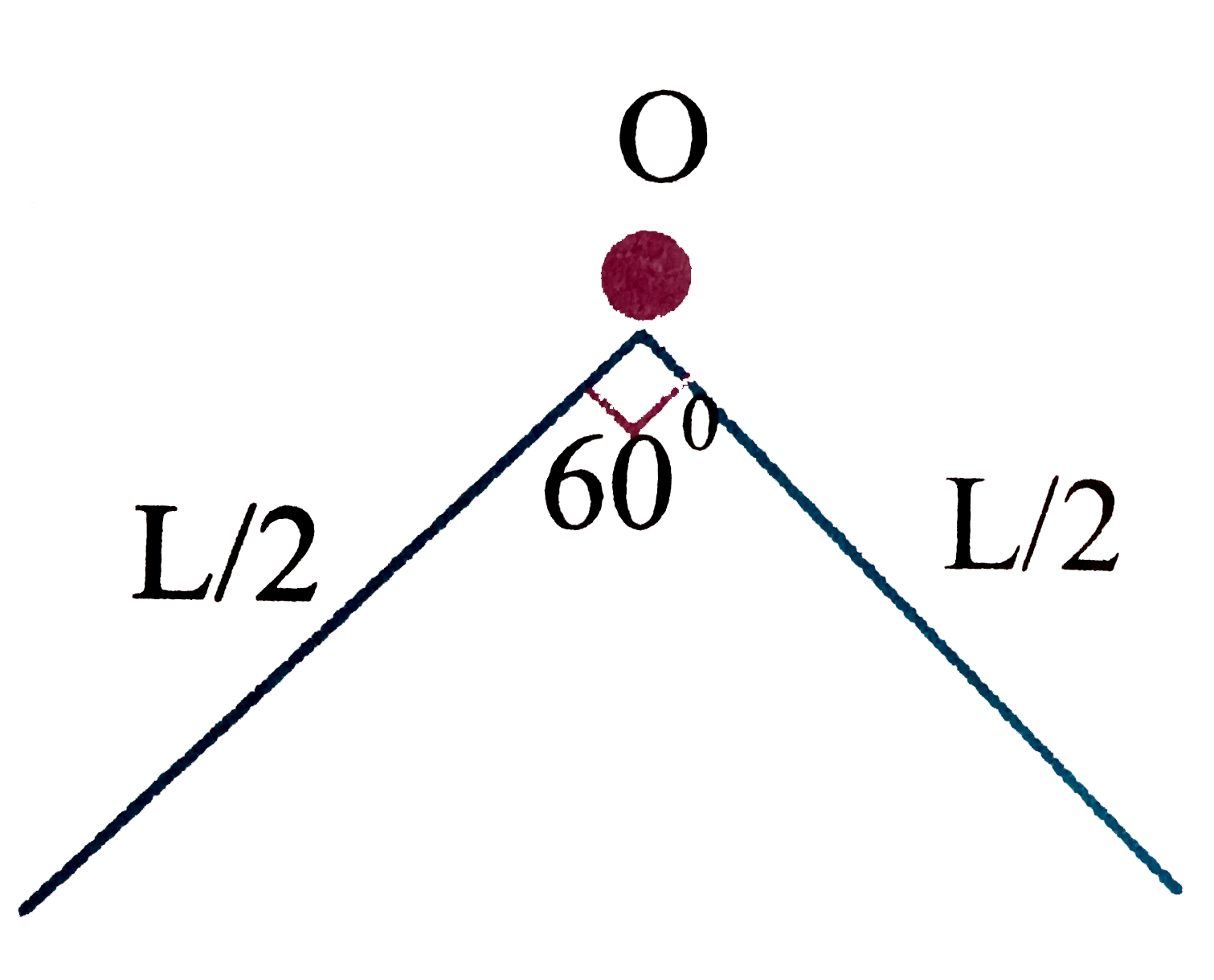 View Solution
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View Solution

