Two identical rods are connected between two containers. One of them is at 100∘C containing water and another is at 0∘C containing ice. If rods are connected in parallel then the rate of melting of ice is q1g/s . If they are connected in series then teh rate is q2g/s . The ratio q2/q1 is
2
4
12
14
The correct Answer is:D
To solve the problem, we need to analyze the heat transfer through the rods in both parallel and series configurations and find the ratio of the rates of melting of ice, q2q1.
1. Understanding the Setup:
- We have two identical rods connecting two containers: one with water at 100∘C and the other with ice at 0∘C.
- The rods are made of the same material, so they have the same thermal conductivity k, cross-sectional area A, and length L.
2. Parallel Configuration:
- In the parallel configuration, both rods conduct heat simultaneously.
- The thermal resistance R for each rod is given by:
R=LkA
- For two rods in parallel, the equivalent thermal resistance Req is:
1Req=1R1+1R2=1LkA+1LkA=2kAL
- Therefore, the equivalent resistance is:
Req=L2kA
- The rate of heat transfer dqdt through the rods is given by:
dqdt=ΔTReq=100−0L2kA=200kAL
- This heat is used to melt the ice, so we can relate it to the rate of melting:
dmdt=dqdt⋅1Lf=200kAL⋅1Lf
- Thus, we have:
q1=200kAL⋅1Lf
3. Series Configuration:
- In the series configuration, the heat must pass through both rods sequentially.
- The total thermal resistance is:
Req=R1+R2=LkA+LkA=2LkA
- The rate of heat transfer dqdt is:
dqdt=100−02LkA=100kAL
- This heat is also used to melt the ice:
dmdt=dqdt⋅1Lf=100kAL⋅1Lf
- Thus, we have:
q2=100kAL⋅1Lf
4. Finding the Ratio:
- Now we can find the ratio q2q1:
q2q1=100kAL⋅1Lf200kAL⋅1Lf=100200=12
Conclusion:
The ratio q2q1 is 12.
- We have two identical rods connecting two containers: one with water at 100∘C and the other with ice at 0∘C.
- The rods are made of the same material, so they have the same thermal conductivity k, cross-sectional area A, and length L.
- In the parallel configuration, both rods conduct heat simultaneously.
- The thermal resistance R for each rod is given by:
R=LkA
- For two rods in parallel, the equivalent thermal resistance Req is:
1Req=1R1+1R2=1LkA+1LkA=2kAL
- Therefore, the equivalent resistance is:
Req=L2kA
- The rate of heat transfer dqdt through the rods is given by:
dqdt=ΔTReq=100−0L2kA=200kAL
- This heat is used to melt the ice, so we can relate it to the rate of melting:
dmdt=dqdt⋅1Lf=200kAL⋅1Lf
- Thus, we have:
q1=200kAL⋅1Lf
- In the series configuration, the heat must pass through both rods sequentially.
- The total thermal resistance is:
Req=R1+R2=LkA+LkA=2LkA
- The rate of heat transfer dqdt is:
dqdt=100−02LkA=100kAL
- This heat is also used to melt the ice:
dmdt=dqdt⋅1Lf=100kAL⋅1Lf
- Thus, we have:
q2=100kAL⋅1Lf
- Now we can find the ratio q2q1:
q2q1=100kAL⋅1Lf200kAL⋅1Lf=100200=12
The ratio q2q1 is 12.
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Match the columns
4 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Two identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end connected to the same vessels. Let m1andm2 g/s be the rate of melting of ice in the two cases respectively, the ratio m1m2 is
View SolutionThe effective capacitance of two capacitors of capacitances C1 and C2(C2>C1) connected in parallel is 256 times the effective capacitance when they are connected in series. The ratio C2C1 is
View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is
(a) 12 (b)21 (c)41 (d)14
View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is
(a) 12 (b)21 (c)41 (d)14
View SolutionChoose the correct option:
Two identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is:
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C

Q. What is the temperature of ϕ2?
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C

Q. What is the temperature of ϕ3?
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C
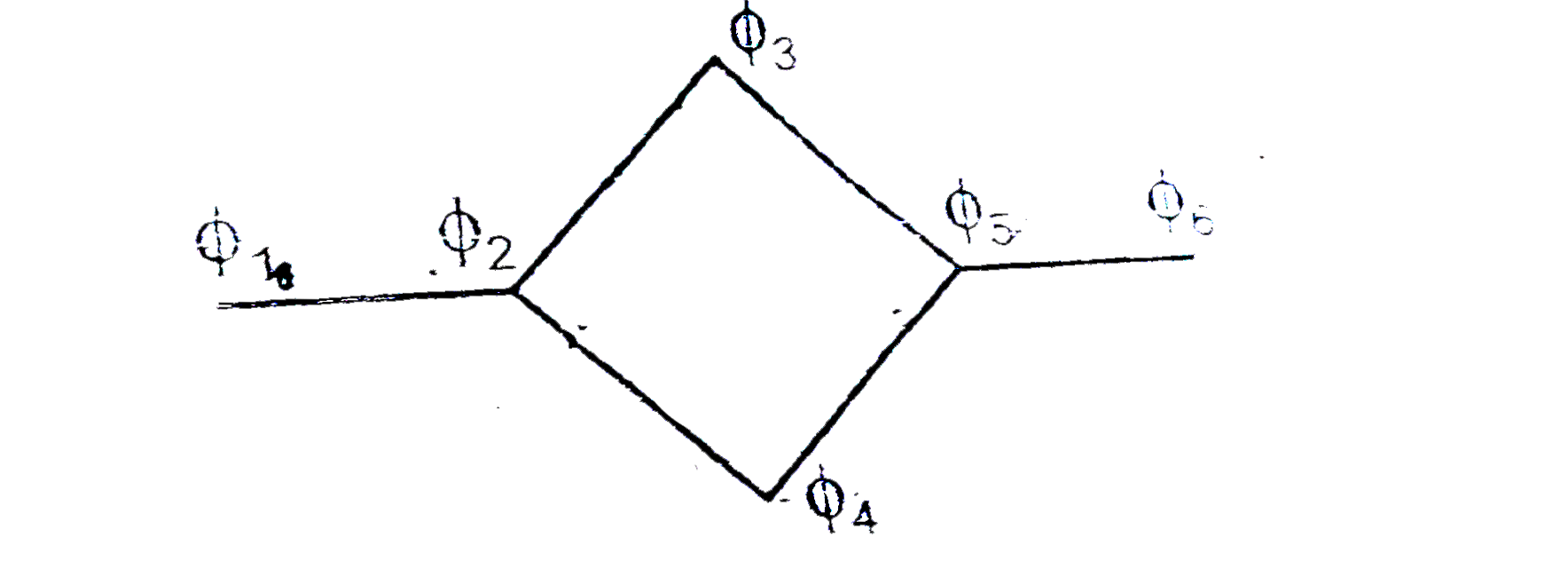
Q. What is the temperature of ϕ5?
View SolutionTwo containers having boiling water and ice are connected through a conducting metal rod. The whole ice melts in time T. now the rod is cut into two equal parts and both parts are connected in parallel between the containers the time required to melt the same amount of ice will be
View SolutionTwo conducting rods when connected between two points at constant but different temperatures separately, the rate of heat flow through them is q1andq2.
View Solution