The wavelength of a light is of the order of 6400Å. Express this in micron and metre.
To convert the wavelength of light from angstroms to microns and meters, we can follow these steps:
Step 1: Understand the given information
We are given that the wavelength of light is 6400Å (angstroms).
Step 2: Convert angstroms to meters
1 angstrom is equal to 10−10 meters. Therefore, to convert angstroms to meters, we can use the conversion factor:
Wavelength in meters=Wavelength in angstroms×(10−10m/Å)
Substituting the given value:
Wavelength in meters=6400Å×10−10m/Å
Calculating this gives:
Wavelength in meters=6400×10−10m=6.4×10−7m
Step 3: Convert meters to microns
1 micron (µm) is equal to 10−6 meters. Therefore, to convert meters to microns, we can use the conversion factor:
Wavelength in microns=Wavelength in meters×(106µm/m)
Substituting the value we calculated in the previous step:
Wavelength in microns=6.4×10−7m×106µm/m
Calculating this gives:
Wavelength in microns=6.4×10−7×106µm=0.64µm
Final Results
- The wavelength of light in meters is 6.4×10−7m.
- The wavelength of light in microns is 0.64µm.
---
We are given that the wavelength of light is 6400Å (angstroms).
1 angstrom is equal to 10−10 meters. Therefore, to convert angstroms to meters, we can use the conversion factor:
1 micron (µm) is equal to 10−6 meters. Therefore, to convert meters to microns, we can use the conversion factor:
- The wavelength of light in meters is 6.4×10−7m.
- The wavelength of light in microns is 0.64µm.
Topper's Solved these Questions
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Check Point 1.1
25 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Check Point 1.2
10 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
Similar Questions
The wavelength of light visible to eye is of the order of
View SolutionThe wavelength of light of a particular colour is 5800 Å. Express it in.
(i) nanometre and (ii)metre
View SolutionThe wavelength of light is 5000 Å , express it in nm .
View SolutionThe wavelength of light is 5000 Å , express it in m .
View SolutionThe wavelength of a blue light is 4800 Å. Calculate the frequency and wave number of this light.
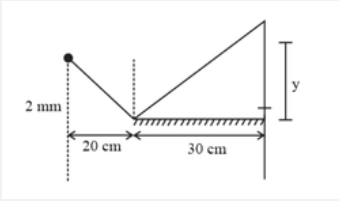
View SolutionA plane mirror of length 30 cm is placed horizontally along with a vertical screen. A monochromatic point source of light is placed 20 cm to the left off the left edge of the mirror, at a height of 2 mm above the plane of the mirror. If the wavelength of light used is 6400Å, then find the number of complete bright fringes formed.
View SolutionThe wavelength of light is 840 nm. What is its wavelength in Å ?
View SolutionIf in a photoelectric cell , the wavelength of incident light is changed from 4000 Å to 3000 Å then change in stopping potential will be
View SolutionOn decreasing the wavelength of incident light from 8000 Å to 4000 Å. The intensity of the scattered light in Rayleigh scattering will become _________ time the initial scattered intensity.
View SolutionIf the wavelength of light used is 6000 Å. The angular resolution of telescope of objective lens having diameter 10 cm is ______ rad.
View Solution
