Resultant of which of a following may be equal to zero?
10N,10N,10N
10N,10N,25N
10N,10N,35N
None of these
The correct Answer is:A
To determine which set of vectors can have a resultant equal to zero, we need to analyze the options provided based on the triangle inequality theorem. The triangle inequality states that for any three sides to form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
1. Identify the Options: We have four options of vectors:
- Option 1: 10N, 10N, 10N
- Option 2: 10N, 10N, 25N
- Option 3: 10N, 10N, 35N
- Option 4: None of these
2. Apply the Triangle Inequality:
- For three vectors to have a resultant of zero, they must be able to form a closed triangle. We will check each option to see if they satisfy the triangle inequality.
3. Check Option 1 (10N, 10N, 10N):
- Check: 10 + 10 > 10 (True)
- Check: 10 + 10 > 10 (True)
- Check: 10 + 10 > 10 (True)
- Since all conditions are satisfied, these vectors can form a triangle, and thus, the resultant can be zero.
4. Check Option 2 (10N, 10N, 25N):
- Check: 10 + 10 > 25 (False)
- Since this condition is not satisfied, these vectors cannot form a triangle, and thus, the resultant cannot be zero.
5. Check Option 3 (10N, 10N, 35N):
- Check: 10 + 10 > 35 (False)
- Since this condition is not satisfied, these vectors cannot form a triangle, and thus, the resultant cannot be zero.
6. Check Option 4 (None of these):
- Since we found that Option 1 can have a resultant of zero, this option is incorrect.
7. Conclusion: The only option where the resultant can be equal to zero is Option 1: 10N, 10N, 10N.
Final Answer:
The resultant of the vectors in Option 1 (10N, 10N, 10N) may be equal to zero.
---
- Option 1: 10N, 10N, 10N
- Option 2: 10N, 10N, 25N
- Option 3: 10N, 10N, 35N
- Option 4: None of these
- For three vectors to have a resultant of zero, they must be able to form a closed triangle. We will check each option to see if they satisfy the triangle inequality.
- Check: 10 + 10 > 10 (True)
- Check: 10 + 10 > 10 (True)
- Check: 10 + 10 > 10 (True)
- Since all conditions are satisfied, these vectors can form a triangle, and thus, the resultant can be zero.
- Check: 10 + 10 > 25 (False)
- Since this condition is not satisfied, these vectors cannot form a triangle, and thus, the resultant cannot be zero.
- Check: 10 + 10 > 35 (False)
- Since this condition is not satisfied, these vectors cannot form a triangle, and thus, the resultant cannot be zero.
- Since we found that Option 1 can have a resultant of zero, this option is incorrect.
The resultant of the vectors in Option 1 (10N, 10N, 10N) may be equal to zero.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following may best be called aromatic ?
A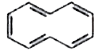 B
B C
C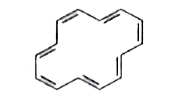 D
D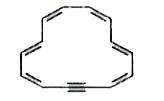
- Question 2 - Select One or More
Which of the following may be classifed as an acetal?
A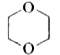 B
B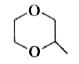 C
C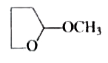 D
D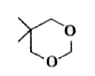
Which of the following may cause water blooms
View SolutionWhich of the following has value zero:
View SolutionWhich of the following has/have value equal to zero ?
View SolutionWhich of the following ligands may be flexidentate ?
View SolutionWhich of the following has zero valency?
View Solutionwhich of the following pairs may give equal numerical values of the temperature of a body?
View Solution

