A particle undergoes three successive displacements given by s1=√2 m north - east , s2=2 m due south and s3=4m,30∘ north of west , then magnitude of net displacement is
√14+4√3
√14−4√3
√4
None of these
The correct Answer is:B
To solve the problem of finding the magnitude of the net displacement of a particle undergoing three successive displacements, we can follow these steps:
Step 1: Define the Displacements
The displacements are given as:
- s1=√2 m (North-East)
- s2=2 m (South)
- s3=4 m (30° North of West)
Step 2: Break Down Each Displacement into Components
1. Displacement s1:
- North-East means it makes a 45° angle with both the North and East axes.
- Components:
s1x=s1cos(45∘)=√2⋅1√2=1 m (East)
s1y=s1sin(45∘)=√2⋅1√2=1 m (North)
2. Displacement s2:
- Due South means it only has a negative y-component.
- Components:
s2x=0 m
s2y=−2 m
3. Displacement s3:
- 30° North of West means it has both negative x-component and positive y-component.
- Components:
s3x=−s3cos(30∘)=−4⋅√32=−2√3 m
s3y=s3sin(30∘)=4⋅12=2 m
Step 3: Sum the Components
Now, we can sum the x and y components of all three displacements to find the net displacement.
- Net x-component:
snet,x=s1x+s2x+s3x=1+0−2√3=1−2√3
- Net y-component:
snet,y=s1y+s2y+s3y=1−2+2=1
Step 4: Calculate the Magnitude of the Net Displacement
The magnitude of the net displacement snet can be calculated using the Pythagorean theorem:
snet=√s2net,x+s2net,y
Substituting the values:
snet=√(1−2√3)2+(1)2
Step 5: Simplify the Expression
Calculating the squares:
(1−2√3)2=1−4√3+12=13−4√3
So,
snet=√(13−4√3)+1=√14−4√3
Final Answer
The magnitude of the net displacement is:
√14−4√3 m
The displacements are given as:
- s1=√2 m (North-East)
- s2=2 m (South)
- s3=4 m (30° North of West)
1. Displacement s1:
- North-East means it makes a 45° angle with both the North and East axes.
- Components:
s1x=s1cos(45∘)=√2⋅1√2=1 m (East)
s1y=s1sin(45∘)=√2⋅1√2=1 m (North)
- Due South means it only has a negative y-component.
- Components:
s2x=0 m
s2y=−2 m
- 30° North of West means it has both negative x-component and positive y-component.
- Components:
s3x=−s3cos(30∘)=−4⋅√32=−2√3 m
s3y=s3sin(30∘)=4⋅12=2 m
Now, we can sum the x and y components of all three displacements to find the net displacement.
snet,x=s1x+s2x+s3x=1+0−2√3=1−2√3
snet,y=s1y+s2y+s3y=1−2+2=1
The magnitude of the net displacement snet can be calculated using the Pythagorean theorem:
snet=√s2net,x+s2net,y
Substituting the values:
snet=√(1−2√3)2+(1)2
Calculating the squares:
(1−2√3)2=1−4√3+12=13−4√3
So,
snet=√(13−4√3)+1=√14−4√3
The magnitude of the net displacement is:
√14−4√3 m
Topper's Solved these Questions
Similar Questions
A man first moves 3 m due east , them 6 m due north and finally 7 m due west , then the magnitude of the resultant displacement is (in metre)
View SolutionA spider crawls 1 m due north , 2 m due east and then climbs 3 m vertically on a wall . What is the magnitude of the resultant dispalcemen ?
View Solution
Knowledge Check
- Question 1 - Select One
A man goes 10 m towards North, then 20 m towards east then displacement is
A22.5 mB25 mC25.5 mD30 m
A bird moves in such a way that it has a displacement of 12 m towards east, 5 m towards north and 9 m vertically upwards. Find the magnitude of its displacement.
View SolutionRepresent graphically
(a) A displacement of 50 km, 30∘ south of west
(b) A displacement of 40 km, 60∘ north of eastView SolutionAn aeroplane flies 400 m north and 300m south and then flies 1200 m upwards then net displacement is
View SolutionA man moves towards 3m north then 4 m towards east and finally 5 m towards 37∘ south of west. His displacement from origin is :-
View SolutionRam moves in east direction at a speed of 6 m/s and Shyam moves 30∘ east of north at a speed of 6 m/s. The magnitude of their relative velocity is
View SolutionA particle is moving eastwards with a speed of 6 m/s. After 6 s, the particle is found to be moving with same speed in a direction 60∘ north of east. The magnitude of average acceleration in this interval of time is
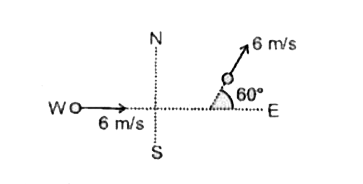 View Solution
View SolutionAboy Walks 4m east and then 3m south .Find the displacement of the boy.
View Solution

