A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
0.01 m
0.1 m
0.2 m
0.5 m
The correct Answer is:B
To solve the problem, we will use the principle of conservation of energy. The kinetic energy of the body will be converted into the elastic potential energy of the spring when the body comes to rest after compressing the spring.
1. Convert Mass to Kilograms:
The mass of the body is given as 0.1 g. We need to convert this to kilograms because the SI unit of mass is kilograms.
m=0.1 g=0.11000 kg=0.0001 kg
Hint: Remember to convert grams to kilograms by dividing by 1000.
2. Calculate Initial Kinetic Energy:
The kinetic energy (KE) of the body can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×0.0001 kg×(10 m/s)2=12×0.0001×100=0.005 J
Hint: Use the formula for kinetic energy and make sure to square the velocity.
3. Set Up the Equation for Elastic Potential Energy:
The elastic potential energy (EPE) stored in the spring when it is compressed by a distance x is given by:
EPE=12kx2
where k is the spring constant (1000 N/m). Since the body comes to rest, the kinetic energy is converted entirely into elastic potential energy:
KE=EPE
Thus,
0.005=12×1000×x2
Hint: Remember that the kinetic energy is equal to the potential energy stored in the spring at maximum compression.
4. Solve for x2:
Rearranging the equation gives:
0.005=500x2
Dividing both sides by 500:
x2=0.005500=0.00001
Hint: Make sure to isolate x2 by dividing both sides by the spring constant.
5. Calculate x:
Taking the square root of both sides:
x=√0.00001=0.003162 m
Hint: When you take the square root, ensure you have the correct units.
6. Convert to Centimeters (if necessary):
To express the compression in centimeters:
x=0.003162 m×100=0.3162 cm
Hint: Remember that 1 m = 100 cm for unit conversion.
Final Answer:
The compression of the spring is approximately 0.003162 m or 0.3162 cm.
The mass of the body is given as 0.1 g. We need to convert this to kilograms because the SI unit of mass is kilograms.
m=0.1 g=0.11000 kg=0.0001 kg
The kinetic energy (KE) of the body can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×0.0001 kg×(10 m/s)2=12×0.0001×100=0.005 J
The elastic potential energy (EPE) stored in the spring when it is compressed by a distance x is given by:
EPE=12kx2
where k is the spring constant (1000 N/m). Since the body comes to rest, the kinetic energy is converted entirely into elastic potential energy:
KE=EPE
Thus,
0.005=12×1000×x2
Rearranging the equation gives:
0.005=500x2
Dividing both sides by 500:
x2=0.005500=0.00001
Taking the square root of both sides:
x=√0.00001=0.003162 m
To express the compression in centimeters:
x=0.003162 m×100=0.3162 cm
The compression of the spring is approximately 0.003162 m or 0.3162 cm.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.310videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISES(TAKING IT TOGETHER)83videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.120videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions11videos
WORK, POWER AND ENERGY
Similar Questions
A body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be
 View Solution
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is
 View Solution
View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
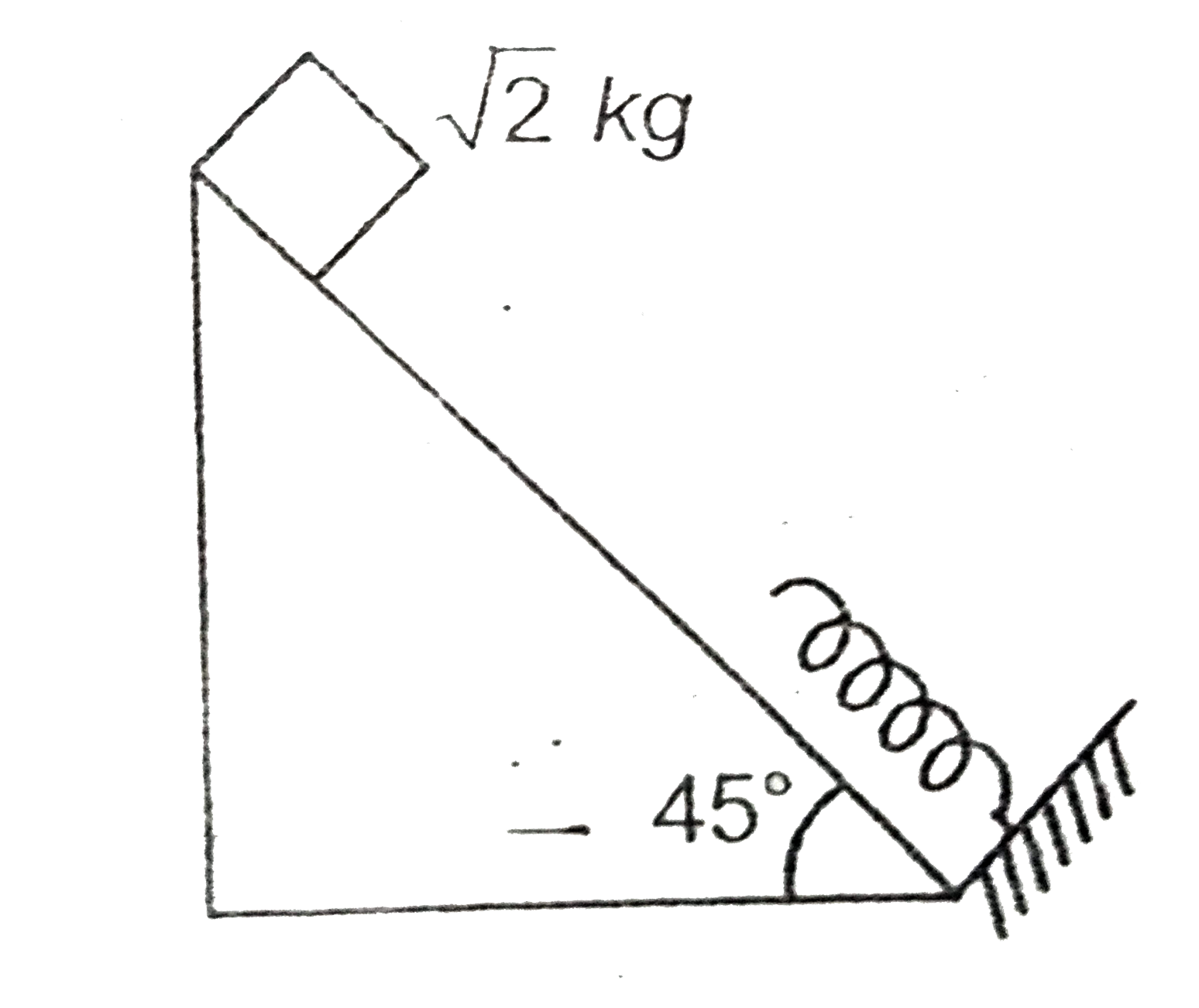 View Solution
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
 View Solution
View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100N/m and block comes to rest after compressing spring by 1 m, find the distance travelled by the block before it comes t o rest.
 View Solution
View SolutionAn elevatore is moving up with a constant velocity. Two different masses are attached to two different springs of same spring constant. Say you do two operations expanding the spring or compressing the spring by the same distance. Which operation consumes more energy: expanding the spring or compressing it?
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.
 View Solution
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?
 View Solution
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest
 View Solution
View Solution

