A particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
The motion of the particle is simple harmonic
The motion of the particle is periodic
The speed of the particle at the centre of earth equals √2GM(R+h) , where R and M are the radius and mass of the earth respectively
The speed of the particle at the centre of earth equals √GM(R+3h)R(R+h), where R and M are the radius and mass of the earth respectively
The correct Answer is:D
To solve the problem of a particle of mass m dropped from a height h above a hole dug through the Earth along its diameter, we can analyze the motion of the particle as it falls and then moves through the Earth.
1. Understanding the Problem:
- A particle is dropped from a height h above the Earth's surface into a hole that goes through the Earth's center. We need to analyze its motion as it falls and passes through the Earth.
2. Potential Energy at Height h:
- The potential energy U of the particle at height h above the Earth's surface is given by:
Uh=mgh
- Here, g is the acceleration due to gravity at the Earth's surface.
3. Potential Energy at the Center of the Earth:
- When the particle reaches the center of the Earth, we need to consider the gravitational potential energy at that point. The potential energy at the center can be derived from the gravitational potential energy formula:
Uc=−GMmR
- Where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
4. Using Conservation of Energy:
- The total mechanical energy is conserved. Therefore, the potential energy at height h will equal the potential energy at the center plus the kinetic energy at the center:
mgh=−GMmR+12mv2
- Rearranging this equation gives us:
12mv2=mgh+GMmR
5. Finding the Velocity v:
- We can simplify the equation to find the velocity v when the particle reaches the center:
v2=2gh+2GMR
- Thus, the velocity v is:
v=√2gh+2GMR
6. Final Expression:
- The final expression for the velocity of the particle when it reaches the center of the Earth is:
v=√2g(h+R2)
Conclusion:
The particle, when dropped from height h, will have a velocity given by the derived formula when it reaches the center of the Earth.
- A particle is dropped from a height h above the Earth's surface into a hole that goes through the Earth's center. We need to analyze its motion as it falls and passes through the Earth.
- The potential energy U of the particle at height h above the Earth's surface is given by:
Uh=mgh
- Here, g is the acceleration due to gravity at the Earth's surface.
- When the particle reaches the center of the Earth, we need to consider the gravitational potential energy at that point. The potential energy at the center can be derived from the gravitational potential energy formula:
Uc=−GMmR
- Where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
- The total mechanical energy is conserved. Therefore, the potential energy at height h will equal the potential energy at the center plus the kinetic energy at the center:
mgh=−GMmR+12mv2
- Rearranging this equation gives us:
12mv2=mgh+GMmR
- We can simplify the equation to find the velocity v when the particle reaches the center:
v2=2gh+2GMR
- Thus, the velocity v is:
v=√2gh+2GMR
- The final expression for the velocity of the particle when it reaches the center of the Earth is:
v=√2g(h+R2)
The particle, when dropped from height h, will have a velocity given by the derived formula when it reaches the center of the Earth.
Similar Questions
A particle of mass m is dropped from a height h above the ground. At the same time another particle of mass 2m is thrown vertically upwards from the ground with a speed of √gh . If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of √hg is:
View SolutionA particle of mass m is dropped from a height h above the ground. At the same time another particle of mass 2m is thrown vertically upwards from the ground with a speed of √gh . If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of √hg is :
View SolutionA particle of mass m is dropped from a height h above the ground. Simultaneously another particle of the same mass is thrown vertically upwards from the ground with a speed of√2gh. If they collide head-on completely inelastically, then the time taken for the combined mass to reach the ground is
View SolutionA particle of mass 2m is dropped from a height 80 m above the ground. At the same time another particle of mass m is thrown vertically upwards from the ground with a speed of 40 m/s. If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of second is:
View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.

At what time will it enter the hole at A
View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.

What time will it take to move from A to B?
View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.
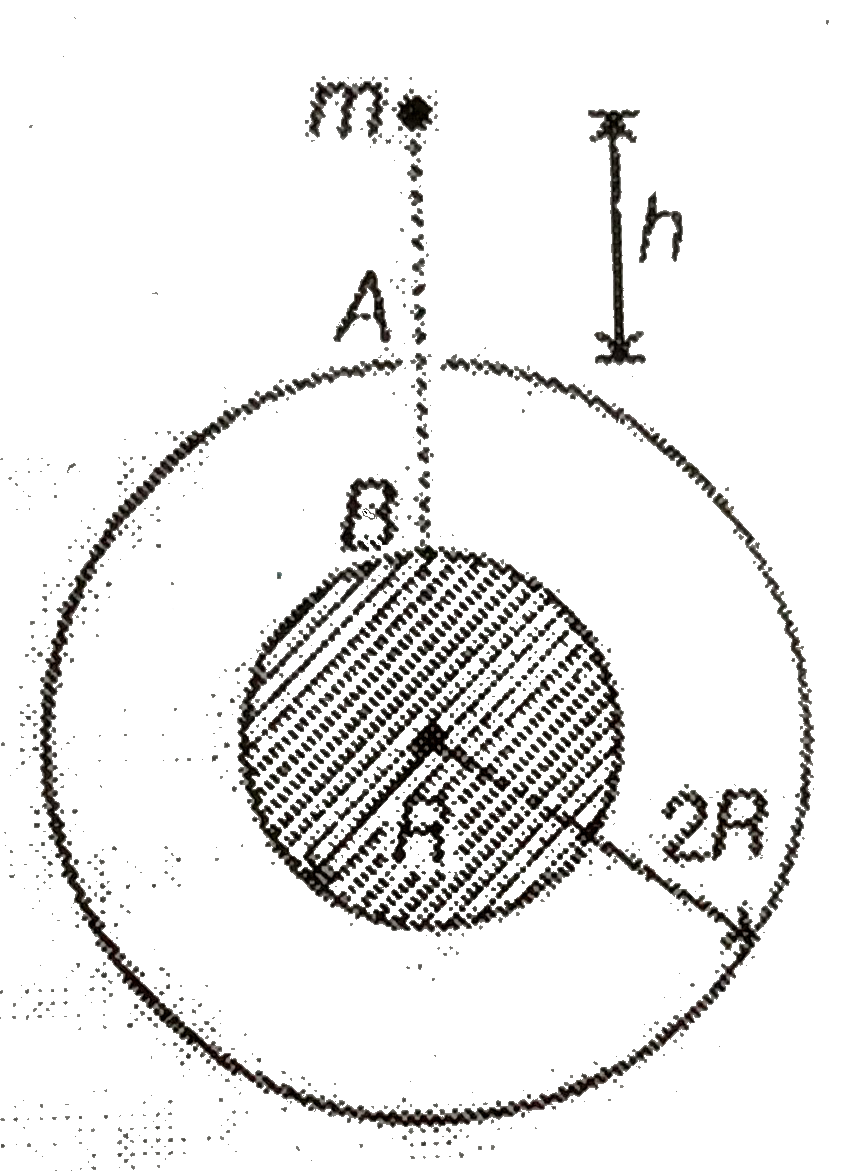
What speed will it collide at B?
View SolutionA ball of mass m is dropped from a height h equal to the radius of the earth above the tunnel dug through the earth as shows in the figure. Choose the correct options. (Mass of earth =M)

View Solution_E01_069_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole inn the shell.
QIn what time will it enter the hole at A
View Solution_S01_036_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass and radius 2R as shown. A small particle of mass m is relased from rest from a height h(<<R) above the shell. There is a hole in the shell.
Q. In what time will it enter the hole at A
View Solution
