A block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
2T
√2T
T√2
T2
The correct Answer is:D
To solve the problem step by step, we will analyze the situation of the spring and the mass in detail.
Step 1: Understand the initial conditions
We have a block of mass M suspended from a spring with a time period T. The time period of a mass-spring system is given by the formula:
T=2π√Mk
where k is the spring constant.
Step 2: Cut the spring into two equal parts
When the spring is cut into two equal parts, each part will have a new length of L2 (where L is the original length of the spring).
Step 3: Determine the new spring constant
The spring constant of a spring is inversely proportional to its length. When the length of the spring is halved, the spring constant doubles. Therefore, if the original spring constant is k, the new spring constant k′ for each half is:
k′=2k
Step 4: Calculate the new time period
Now, we will find the new time period T′ when the mass M is suspended from one of the cut springs. The time period for the new spring system is given by:
T′=2π√Mk′
Substituting k′=2k into the equation gives:
T′=2π√M2k
Step 5: Relate the new time period to the original time period
We can factor out the √2 from the equation:
T′=2π√Mk⋅1√2=T√2
where T=2π√Mk is the original time period.
Conclusion
Thus, the new time period of oscillation when the mass M is suspended from one part of the spring is:
T′=T√2
We have a block of mass M suspended from a spring with a time period T. The time period of a mass-spring system is given by the formula:
T=2π√Mk
where k is the spring constant.
When the spring is cut into two equal parts, each part will have a new length of L2 (where L is the original length of the spring).
The spring constant of a spring is inversely proportional to its length. When the length of the spring is halved, the spring constant doubles. Therefore, if the original spring constant is k, the new spring constant k′ for each half is:
k′=2k
Now, we will find the new time period T′ when the mass M is suspended from one of the cut springs. The time period for the new spring system is given by:
T′=2π√Mk′
Substituting k′=2k into the equation gives:
T′=2π√M2k
We can factor out the √2 from the equation:
T′=2π√Mk⋅1√2=T√2
where T=2π√Mk is the original time period.
Thus, the new time period of oscillation when the mass M is suspended from one part of the spring is:
T′=T√2
Similar Questions
The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
View SolutionA mass m is suspended from a spring of force constant k. The period of oscillation is T0 The spring is cut into 4 equal parts: The same mass m is suspended from one of the parts. What is the new period?
View SolutionA spring has a certain mass suspended from it and its period for vertical oscillations is T1. The spring is now cut into two equal halves and the same mass is suspended from one of the half. The period of vertical oscillation is now T2. The ratio of T2/T1 is
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionThe periodic time of a mass suspended by a spring (force constant k) is T. The spring be cut into three equal pieces. If the same mass be suspended from one piece, what will be the periodic time ?
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
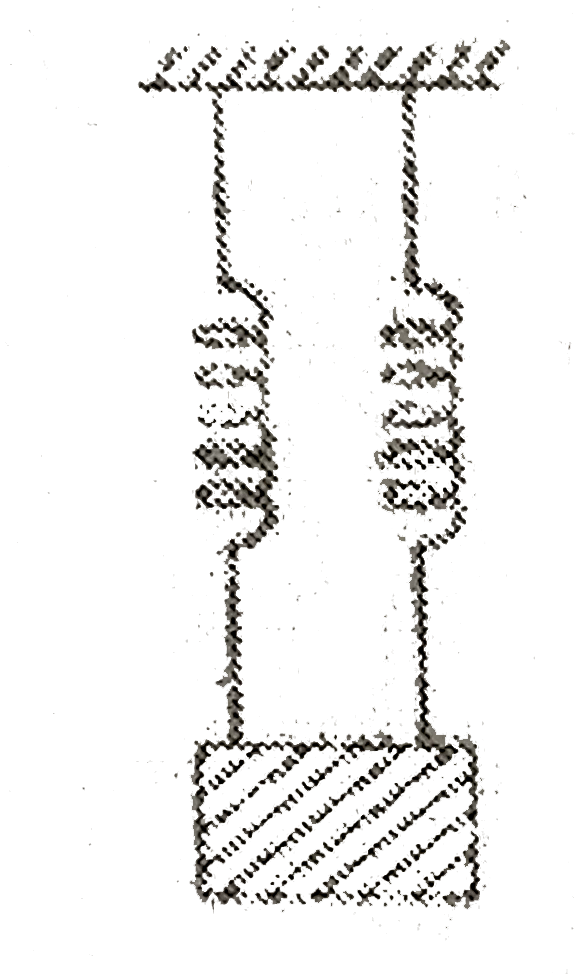 View Solution
View SolutionA weightless spring has a force constant k oscillates with frequency f when a mass m is suspended from it The spring is cut into three equal parts and a mass 3 m is suspended from it The frequency of oscillation of one part will now become
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now ,the spring is cut in half and the two halves are used to support the same object, as shown in figure. The new period of oscillation is .
 .View Solution
.View Solution

