Calcualte rms value of current and voltages for the giving cases
i) I = 4+3sinωt
ii) V = 5+2cosωt
(iii) i=2+3sinωt=2cosωt
iv) V=cosωt+2cos2ωt
To solve the problem of calculating the RMS (Root Mean Square) values of current and voltage for the given cases, we will follow these steps:
Step 1: Understand the RMS Value Calculation
The RMS value of a constant is the constant itself, and the RMS value of a sinusoidal function can be calculated using the formula:
- For a sine function: Irms=I0√2
- For a cosine function: Vrms=V0√2
Step 2: Calculate RMS for Each Case
Case (i): I=4+3sin(ωt)
1. The constant part is 4.
2. The RMS value of 3sin(ωt) is 3√2.
3. Therefore, the total RMS value is:
Irms=4+3√2
Case (ii): V=5+2cos(ωt)
1. The constant part is 5.
2. The RMS value of 2cos(ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=5+2√2
Case (iii): I=2+3sin(ωt)+2cos(ωt)
1. The constant part is 2.
2. The RMS value of 3sin(ωt) is 3√2.
3. The RMS value of 2cos(ωt) is 2√2.
4. Therefore, the total RMS value is:
Irms=2+3√2+2√2=2+5√2
Case (iv): V=cos(ωt)+2cos(2ωt)
1. The RMS value of cos(ωt) is 1√2.
2. The RMS value of 2cos(2ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=1√2+2√2=3√2
Final Results
1. For case (i): Irms=4+3√2
2. For case (ii): Vrms=5+2√2
3. For case (iii): Irms=2+5√2
4. For case (iv): Vrms=3√2
The RMS value of a constant is the constant itself, and the RMS value of a sinusoidal function can be calculated using the formula:
- For a sine function: Irms=I0√2
- For a cosine function: Vrms=V0√2
1. The constant part is 4.
2. The RMS value of 3sin(ωt) is 3√2.
3. Therefore, the total RMS value is:
Irms=4+3√2
1. The constant part is 5.
2. The RMS value of 2cos(ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=5+2√2
1. The constant part is 2.
2. The RMS value of 3sin(ωt) is 3√2.
3. The RMS value of 2cos(ωt) is 2√2.
4. Therefore, the total RMS value is:
Irms=2+3√2+2√2=2+5√2
1. The RMS value of cos(ωt) is 1√2.
2. The RMS value of 2cos(2ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=1√2+2√2=3√2
1. For case (i): Irms=4+3√2
2. For case (ii): Vrms=5+2√2
3. For case (iii): Irms=2+5√2
4. For case (iv): Vrms=3√2
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωtAa simple harmonic motion with a period πω.Ba simple harmonic motion with a period 2πωCa periodic, but not simple harmonic motionn with a period πωDa periodic, but not simple harmonic motion with a period 2πω
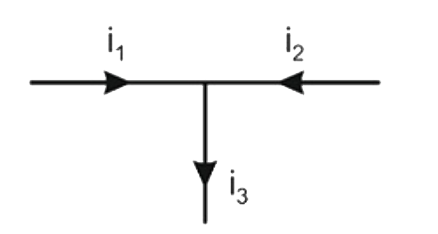
In the given figure, if i1=3sinωtandi2=4cosωt, then i3 is
 View Solution
View Solutionr.m.s. value of current i=3+4sin (omegat+pi//3) is
View SolutionThe electric current in a circuit is given by I = 3 sin ωt+4cosωt. The rms current is
View SolutionFind the rms value of current from t=0 to t=2πω if the current varies as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωtView Solution

