In an ac circuit, the current lags behind the voltage by π/3. The components in the circuit are
R and L
L and C
R and C
only R
The correct Answer is:A
To solve the problem of determining the components in an AC circuit where the current lags behind the voltage by π3, we can analyze the situation step by step.
1. Understanding Phase Relationship:
- In an AC circuit, if the current lags behind the voltage, it indicates that the circuit has inductive characteristics. The phase difference of π3 means that the voltage leads the current by this angle.
2. Identifying Circuit Components:
- The components that can cause a phase difference between voltage and current are resistors (R), inductors (L), and capacitors (C).
- In a purely resistive circuit, the current and voltage are in phase (phase difference = 0).
- In a purely inductive circuit, the current lags the voltage by π2.
- In a purely capacitive circuit, the current leads the voltage by π2.
3. Analyzing the Given Phase Difference:
- Since the current lags the voltage by π3, we need to consider combinations of R and L that can produce this phase difference.
- The presence of a resistor (R) in the circuit allows for a phase angle that is less than π2 when combined with an inductor (L).
4. Considering the RL Circuit:
- In an RL circuit, the phase angle ϕ can be calculated using the formula:
tan(ϕ)=XLR
where XL is the inductive reactance.
- For ϕ=π3:
tan(π3)=√3
- This indicates that the circuit must have both R and L components to achieve this specific phase difference.
5. Evaluating Other Combinations:
- For an LC circuit, the voltage across the inductor (V_L) and the capacitor (V_C) would lead to a phase difference of π2 or −π2, which does not match our requirement.
- For an RC circuit, the current leads the voltage, which is opposite to what we need.
6. Conclusion:
- The only combination of components that allows the current to lag behind the voltage by π3 is an RL circuit.
Final Answer:
The components in the circuit are R and L (Resistor and Inductor).
- In an AC circuit, if the current lags behind the voltage, it indicates that the circuit has inductive characteristics. The phase difference of π3 means that the voltage leads the current by this angle.
- The components that can cause a phase difference between voltage and current are resistors (R), inductors (L), and capacitors (C).
- In a purely resistive circuit, the current and voltage are in phase (phase difference = 0).
- In a purely inductive circuit, the current lags the voltage by π2.
- In a purely capacitive circuit, the current leads the voltage by π2.
- Since the current lags the voltage by π3, we need to consider combinations of R and L that can produce this phase difference.
- The presence of a resistor (R) in the circuit allows for a phase angle that is less than π2 when combined with an inductor (L).
- In an RL circuit, the phase angle ϕ can be calculated using the formula:
tan(ϕ)=XLR
where XL is the inductive reactance.
- For ϕ=π3:
tan(π3)=√3
- This indicates that the circuit must have both R and L components to achieve this specific phase difference.
- For an LC circuit, the voltage across the inductor (V_L) and the capacitor (V_C) would lead to a phase difference of π2 or −π2, which does not match our requirement.
- For an RC circuit, the current leads the voltage, which is opposite to what we need.
- The only combination of components that allows the current to lag behind the voltage by π3 is an RL circuit.
The components in the circuit are R and L (Resistor and Inductor).
Similar Questions
In a circuit, the current lags behind the voltage by a phase difference of π/2, the circuit will contain which of the following ?
View SolutionIn an LCR circuit R=100ohm. When capacitance C is removed, the current lags behind the voltage by π/3. When inductance L is removed, the current leads the voltage by π/3. The impedence of the circuit is
View SolutionIn a series LCR circuit R=200(Ω) and the voltage and the frequency of the main supply is 220V and 50 Hz respectively. On taking out the capacitance from the circuit the current lags behind the voltage by 30(∘). On taking out the inductor from the circuit the current leads the voltage by 30(∘). The power dissipated in the LCR circuit is
View SolutionA circuit shown in the figure contains a box having either a capacitor or an inductor. The power factor of the circuit is 0.8, while current lags behind the voltage. Then find the inductance/capacitance of the box is S.I. unit (take π=3.2). The circuit draws 1 ampere current.
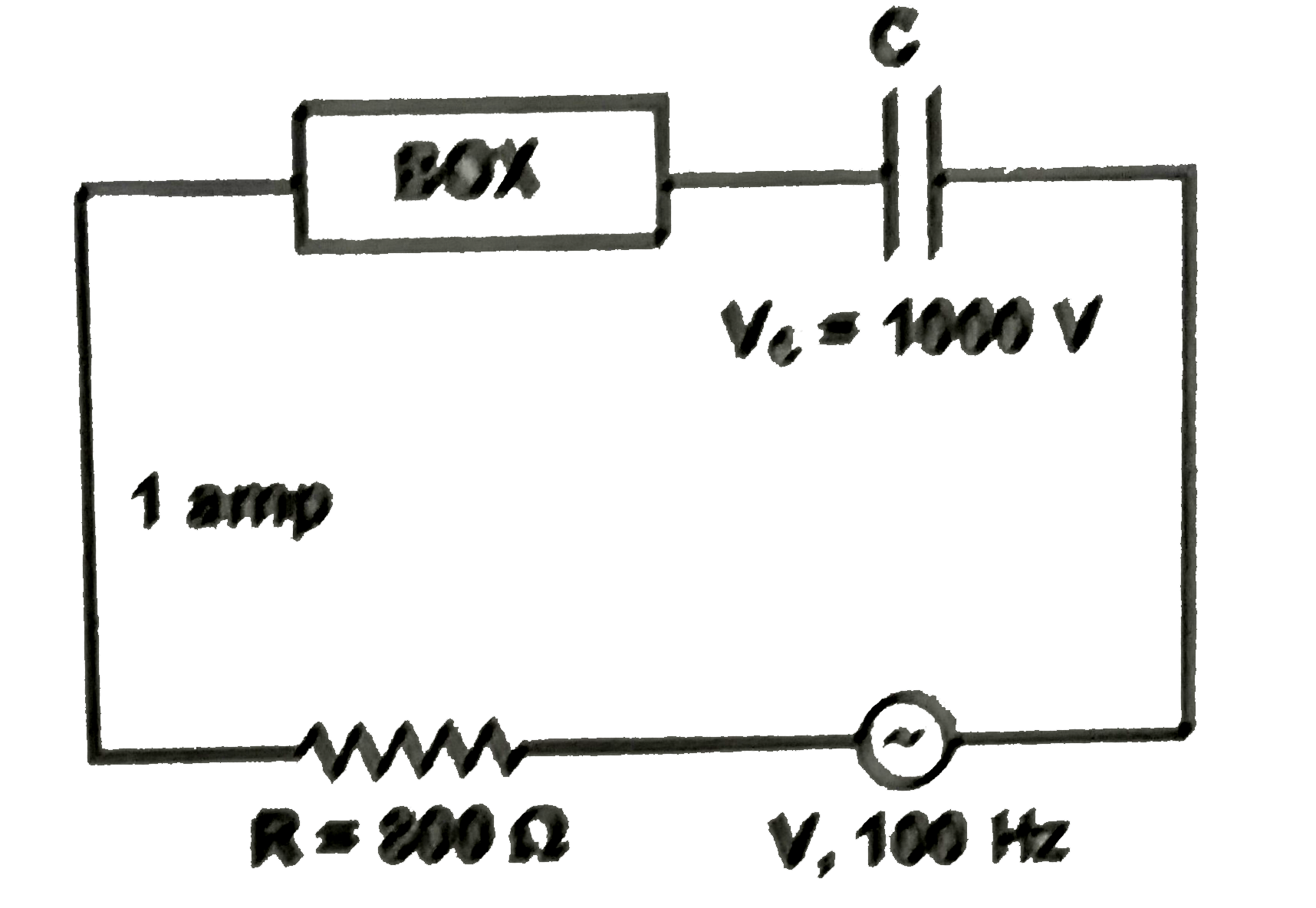
View SolutionAn L−C−R series circuit with 100Ω resistance is connected to an AC source of 200V and angular frequency 300rad/s. When only the capacitance is removed, the current lags behind the voltage by 60∘. When only the inductance is removed the current leads the voltage by 60∘. Calculate the current and the power dissipated in the L−C−R circuit
View SolutionAn L−C−R series circuit with 100Ω resistance is connected to an AC source of 200V and angular frequency 300rad/s. When only the capacitance is removed, the current lags behind the voltage by 60∘. When only the inductance is removed the current leads the voltage by 60∘. Calculate the current and the power dissipated in the L−C−R circuit
View SolutionAn L−C−R series circuit with 100Ω resisance is connected to an AC source of 200V and angular frequency 300rad/s. When only the capacitance is removed, the current lags behind the voltage by 60∘. When only the inductance is removed the current leads the voltage by 60∘. Calculate the current and the power dissipated in the L−C−R circuit
View SolutionAn L−C−R series circuit with 100Ω resistance is connected to an AC source of 200V and angular frequency 300rad/s. When only the capacitance is removed, the current lags behind the voltage by 60∘. When only the inductance is removed the current leads the voltage by 60∘. Calculate the power dissipated in the L−C−R circuit
View SolutionAn LCR circuit contains resistance of 100Ω and a supply of 200V at 300rads−1 angular frequency. If only capacitance is taken out from the circuit and the rest of the circuit is joined, current lags behind the voltage by 60∘ . If, on the other hand , only inductor is taken out,the current leads the voltage by 60o. The current flowing in the circuit is
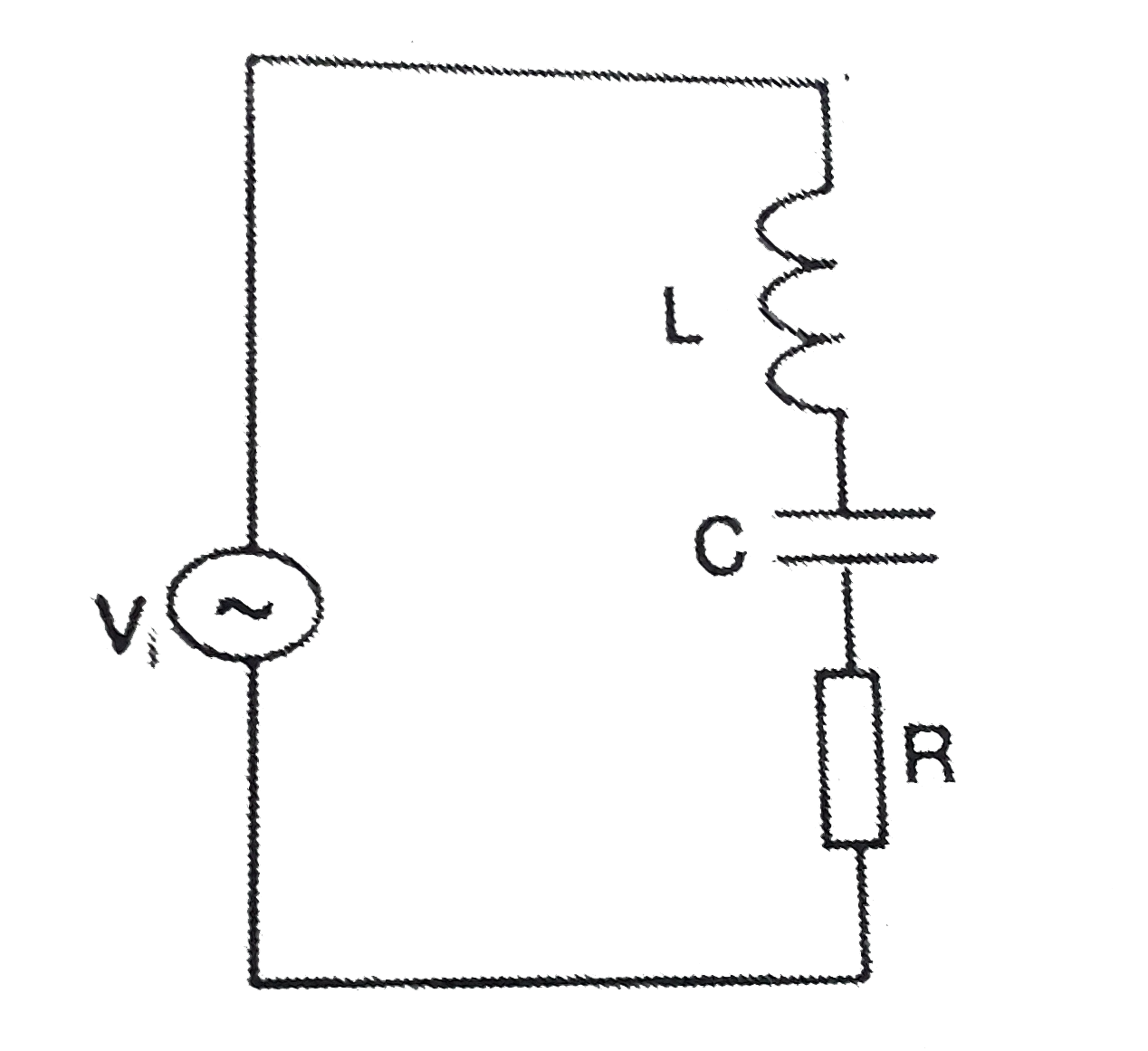
View SolutionIn the following circuit the current is in phase with the applied voltage. Therefore, the current in the circuit and the frequency of the source voltage respectively, are
View Solution
