In an L-C circuit
the energy stored in L as well as in C is magnetic energy
the energy stored in L is magnetic but in C it is electrical
the energy stored in L is electrical but in C it is magnetic
the energy stores in L as well as C is electrical energy
The correct Answer is:B
To solve the problem regarding the energy stored in an LC circuit, we will analyze the energy stored in both the inductor and the capacitor.
1. Identify the Components:
- An LC circuit consists of an inductor (L) and a capacitor (C).
2. Energy Stored in the Inductor:
- The energy (UL) stored in the inductor is given by the formula:
UL=12LI2
- Here, L is the inductance and I is the current flowing through the inductor.
- This energy is stored in the magnetic field created around the inductor.
3. Energy Stored in the Capacitor:
- The energy (UC) stored in the capacitor is given by the formula:
UC=12CV2
- Here, C is the capacitance and V is the voltage across the capacitor.
- This energy is stored in the electric field between the plates of the capacitor.
4. Comparison of Energy Forms:
- The energy stored in the inductor is in the form of magnetic energy.
- The energy stored in the capacitor is in the form of electrical energy.
5. Conclusion:
- Based on the analysis, we can conclude that the energy stored in the inductor is magnetic, while the energy stored in the capacitor is electrical. Therefore, the correct option regarding the energy stored in an LC circuit is:
- Option B: The energy stored in the inductor is magnetic, and in the capacitor, it is electrical.
- An LC circuit consists of an inductor (L) and a capacitor (C).
- The energy (UL) stored in the inductor is given by the formula:
UL=12LI2
- Here, L is the inductance and I is the current flowing through the inductor.
- This energy is stored in the magnetic field created around the inductor.
- The energy (UC) stored in the capacitor is given by the formula:
UC=12CV2
- Here, C is the capacitance and V is the voltage across the capacitor.
- This energy is stored in the electric field between the plates of the capacitor.
- The energy stored in the inductor is in the form of magnetic energy.
- The energy stored in the capacitor is in the form of electrical energy.
- Based on the analysis, we can conclude that the energy stored in the inductor is magnetic, while the energy stored in the capacitor is electrical. Therefore, the correct option regarding the energy stored in an LC circuit is:
- Option B: The energy stored in the inductor is magnetic, and in the capacitor, it is electrical.
Similar Questions
In a L-C circuit, angular frequency at resonance is ω. What will be the new angular frequency when inductor's inductance is made two times and capacitor's capacitance is made four times?
View SolutionFind the phase difference between voltage and current in L-C circuit.
View SolutionThe potential differences across the resistance, capacitance and inductance are 80V,40V and 100V respectively in an L−C−R circuit. The power factor of this circuit is
View SolutionA L-C-R circuit is equivalent to a damped pendulum . In an L-C-R circuit the capacitor is charged to Qo and then connected to the L and R as shown below.
If a student plots graph of the square of maximum charge on the capacitor with time (t) for two different values L1 and L2 (L1gtL2of L), then which of the following represents this graph correctly (plots are schematic and not drawn to scale)

View SolutionIn an L-C-R circuit the AC voltage across R, L and C comes out as 10 V , 10 V and 20 V respectively . The voltage across the enter combination will be
View SolutionA 100V, AC source of frequency of 500Hz is connected to an L-C-R circuit with L=8.1mH,C=12.5μF,R=10Ω all connected in series as shown in figure. What is the quality factor of circuit?

View SolutionIn a series resonant L-C-R circuit, the capacitance is changed from C to 3C. For the same resonant frequency, the inductance should be changed from L to
View SolutionIn an L C R circuit having L = 8 H, C = 0 5μF and R=100Ω in series, the resonance frequency in rad/s is
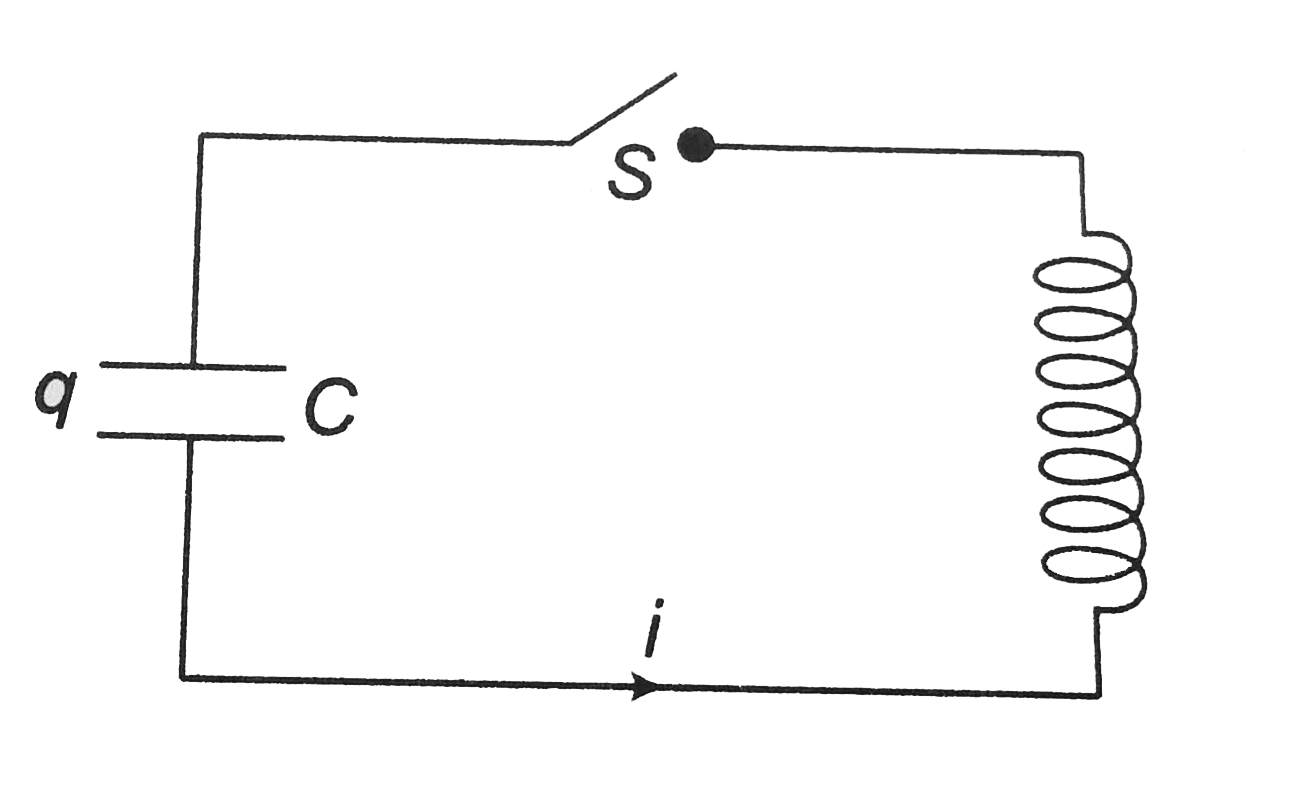
View SolutionIn the L−C circuit shown, C=1μF. With capacitor charged to 100V, switch S is suddenly closed at time t=0. The circuit then oscillates at 103Hz
(a) Calculate co and T
(b) Express q as a function of time
(c) Calculate L
(d) Calculate the average current during the first quarter-cycle.
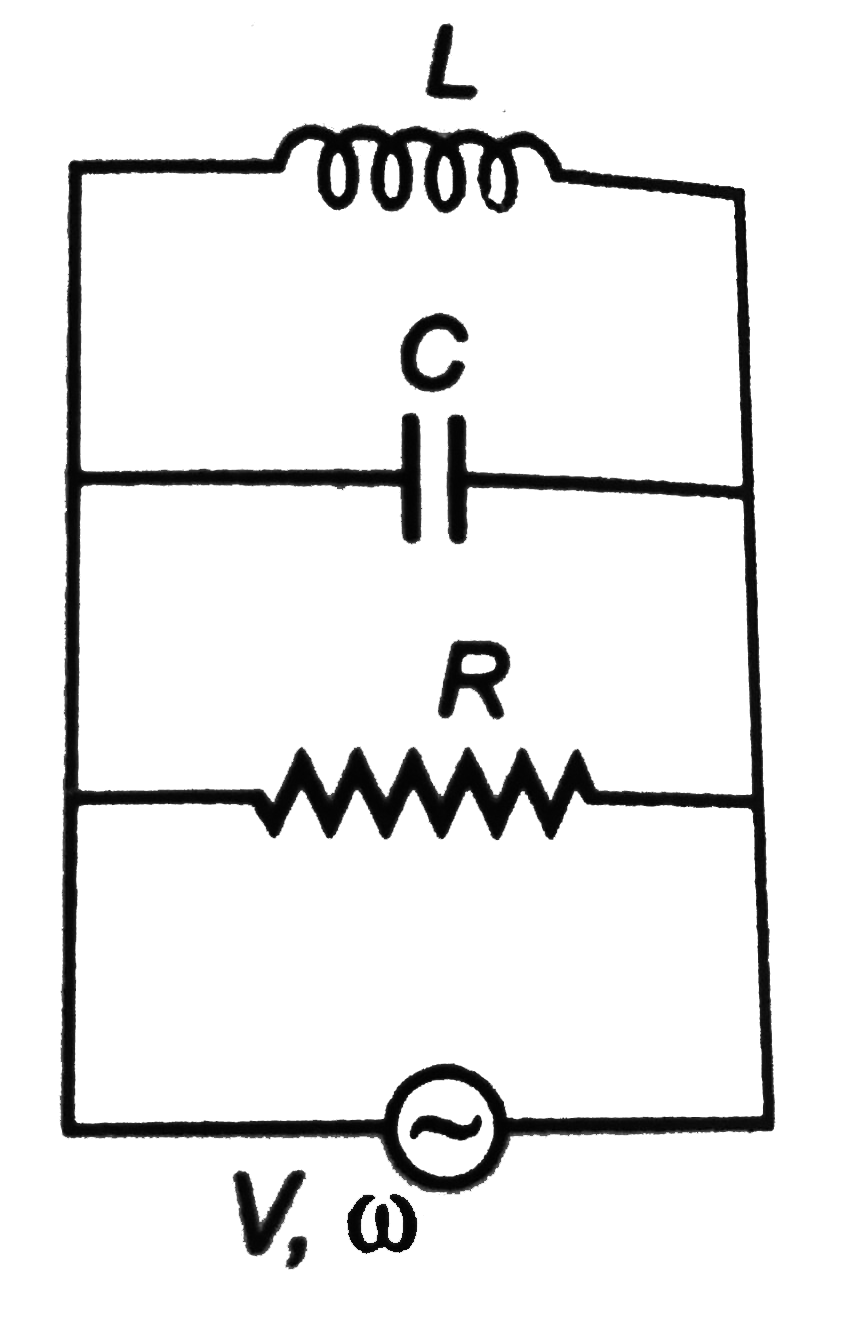
View SolutionConsider in L−C−R circuit as shown in figureure with an AC source of peak value V0 and angular frequency ω. Then the peak value of current through the AC
 .
.
View Solution
