In an LR-circuit, the inductive reactance is equal to the resistance R of the circuit. An e.m.f E=E0cos(ωt) applied to the circuit. The power consumed in the circuit is
E20√2R
E204R
E202R
E208R
The correct Answer is:B
To solve the problem, we need to find the power consumed in an LR circuit where the inductive reactance XL is equal to the resistance R of the circuit. The applied e.m.f. is given by E=E0cos(ωt).
1. Identify the Given Information:
- Inductive reactance: XL=R
- E.M.F: E=E0cos(ωt)
2. Calculate the RMS Values:
- The RMS value of the e.m.f. is given by:
Erms=E0√2
3. Calculate the Impedance Z:
- The impedance in an LR circuit is given by:
Z=√R2+X2L
- Since XL=R, we substitute:
Z=√R2+R2=√2R2=R√2
4. Calculate the RMS Current Irms:
- The RMS current can be calculated using Ohm's law for AC circuits:
Irms=ErmsZ
- Substituting the values we have:
Irms=E0√2R√2=E02R
5. Calculate the Power Factor cos(ϕ):
- The power factor is given by:
cos(ϕ)=RZ
- Substituting Z=R√2:
cos(ϕ)=RR√2=1√2
6. Calculate the Average Power P:
- The average power consumed in the circuit is given by:
P=Erms⋅Irms⋅cos(ϕ)
- Substituting the values we calculated:
P=(E0√2)⋅(E02R)⋅(1√2)
- Simplifying this expression:
P=E20√2⋅2R⋅√2=E204R
Final Result:
The power consumed in the circuit is:
P=E204R
- Inductive reactance: XL=R
- E.M.F: E=E0cos(ωt)
- The RMS value of the e.m.f. is given by:
Erms=E0√2
- The impedance in an LR circuit is given by:
Z=√R2+X2L
- Since XL=R, we substitute:
Z=√R2+R2=√2R2=R√2
- The RMS current can be calculated using Ohm's law for AC circuits:
Irms=ErmsZ
- Substituting the values we have:
Irms=E0√2R√2=E02R
- The power factor is given by:
cos(ϕ)=RZ
- Substituting Z=R√2:
cos(ϕ)=RR√2=1√2
- The average power consumed in the circuit is given by:
P=Erms⋅Irms⋅cos(ϕ)
- Substituting the values we calculated:
P=(E0√2)⋅(E02R)⋅(1√2)
- Simplifying this expression:
P=E20√2⋅2R⋅√2=E204R
The power consumed in the circuit is:
P=E204R
Similar Questions
In the circuit shown in figure, the power consumed is
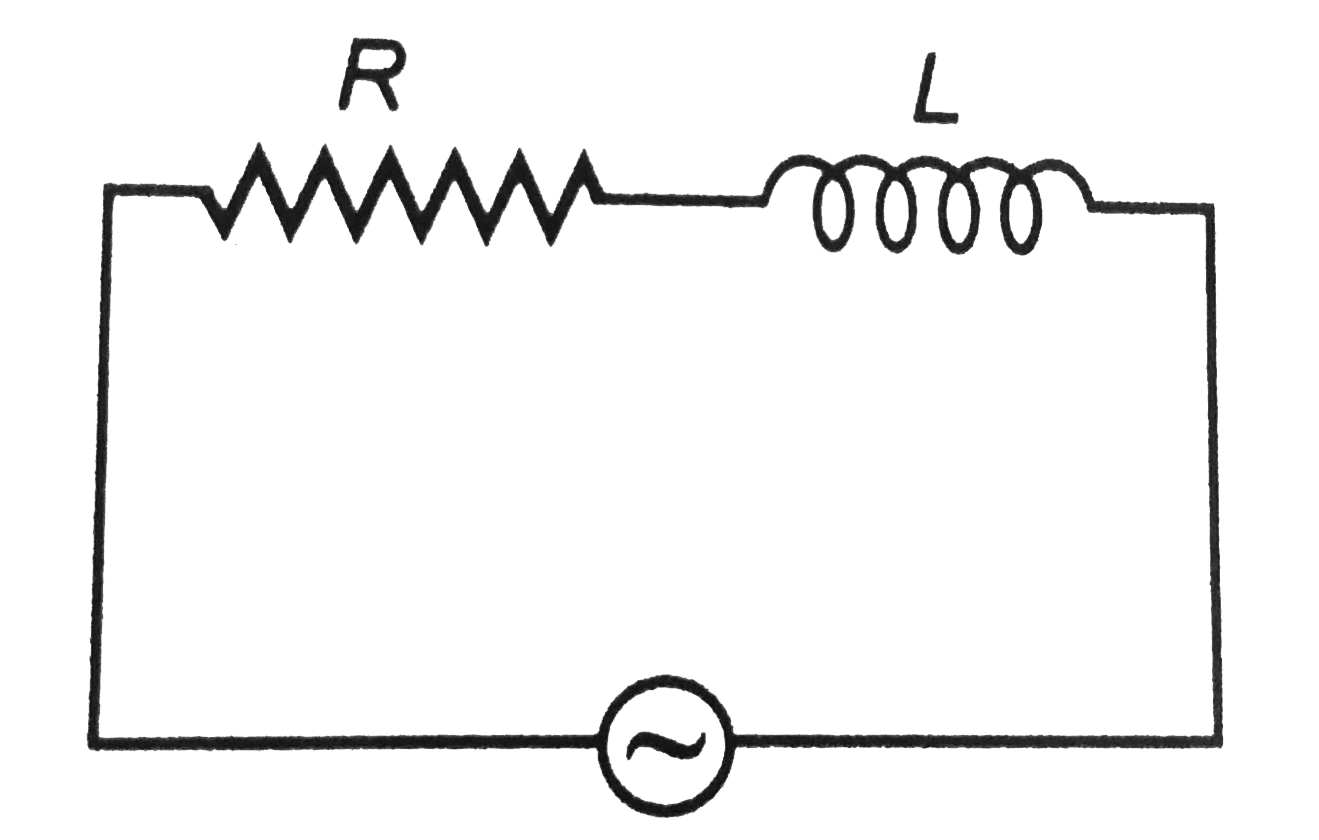 .
.
View SolutionIn L-R circuit, resistance is 8Ω and inductive reactance is 6Ω then impedance is:
View SolutionIn series LCR circuit R=18Ω and impedence is 33Ω. An Vrms voltage 220V is applied across the circuit . The true power consumed in AC circuit is
View SolutionThe impedance of a circuit consister of 3Ωresistance and 4Ω reactance. The power factor of the circuit is
View SolutionThe impedance of a series circuit consists of 3ohm resistance and 4ohm reactance.The power factor of the circuit is
View SolutionThere is no resistance in the inductive circuit Kirchhoff 's voltage law for the circuit is
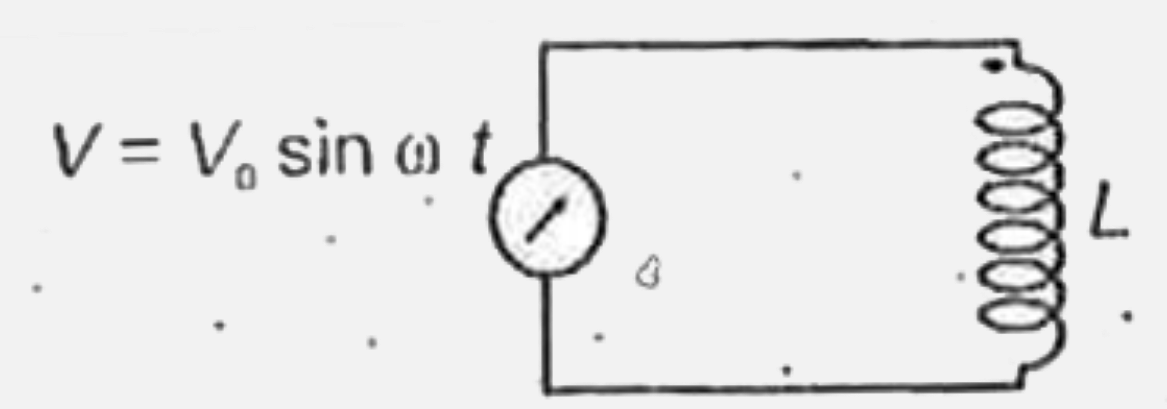
View SolutionThe voltage and current in a series AC circuit are given by V=V0cosωtandI=i0sinωt.
What is the power dissipated in the circuit?
View SolutionAn AC voltage is applied to a resistance R and an inductance L in series. If R and the inductive reactance are both equal to 3Ω, the phase difference between the applied voltage and the current in the circuit is
View SolutionAn AC voltage is applied to a resistance R and an inductance L in series. If R and the inductive reactance are both equal to 3Ω, the phase difference between the applied voltage and the current in the circuit is
View SolutionIn the given circuit, the reading of ideal voltmeter is E/2. The internal resistance of the battery is
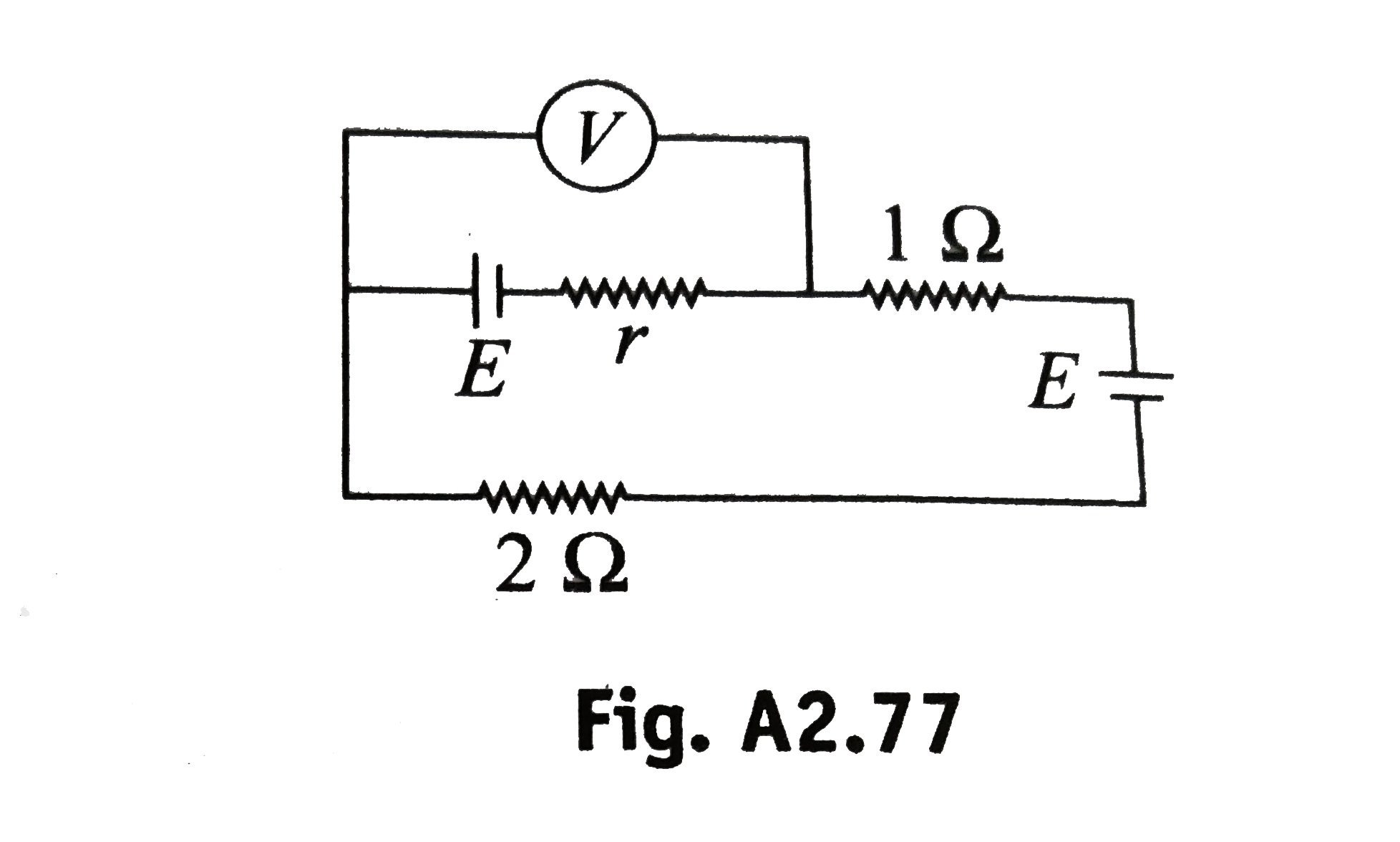
View Solution