A circuit draws 330 W from a 110 V , 60 Hz AC line. The power factor is 0.6 and the current lags the voltage. The capacitance of a series capacitor that will result in a power factor of unity is equal to
31 μF
54 μF
151 μF
201 μF
The correct Answer is:B
To solve the problem step by step, we will follow a structured approach:
Step 1: Calculate the Resistance (R)
Given:
- Power (P) = 330 W
- Voltage (V) = 110 V
Using the formula for power in an AC circuit:
P=V⋅I⋅Power Factor
We can express the current (I) as:
I=PV⋅Power Factor
The power factor is given as 0.6. Therefore, we can calculate the current:
I=330110⋅0.6=33066=5 A
Now, we can find the resistance using Ohm's law:
R=VI=1105=22Ω
Step 2: Relate Power Factor to Resistance and Reactance
The power factor (PF) is given by:
PF=cosϕ=RZ
Where Z is the impedance. Rearranging gives:
Z=RPF=220.6≈36.67Ω
Step 3: Calculate the Inductive Reactance (X_L)
Using the relationship between resistance, reactance, and impedance:
Z2=R2+X2L
Substituting the known values:
(36.67)2=(22)2+X2L
Calculating:
1344.89=484+X2L
X2L=1344.89−484=860.89
XL=√860.89≈29.35Ω
Step 4: Determine the Required Capacitive Reactance (X_C)
To achieve a power factor of unity, we need:
XL=XC
Thus:
XC=29.35Ω
Step 5: Calculate the Capacitance (C)
The capacitive reactance is given by:
XC=12πfC
Rearranging gives:
C=12πfXC
Substituting f=60Hz and XC=29.35Ω:
C=12π⋅60⋅29.35
Calculating:
C=12⋅3.14⋅60⋅29.35≈12⋅3.14⋅1761≈111079.48≈9.03×10−5F=90.3μF
Final Answer
The capacitance of the series capacitor that will result in a power factor of unity is approximately:
C≈90.3μF
Given:
- Power (P) = 330 W
- Voltage (V) = 110 V
P=V⋅I⋅Power Factor
We can express the current (I) as:
I=PV⋅Power Factor
The power factor is given as 0.6. Therefore, we can calculate the current:
I=330110⋅0.6=33066=5 A
R=VI=1105=22Ω
The power factor (PF) is given by:
PF=cosϕ=RZ
Where Z is the impedance. Rearranging gives:
Z=RPF=220.6≈36.67Ω
Using the relationship between resistance, reactance, and impedance:
Z2=R2+X2L
Substituting the known values:
(36.67)2=(22)2+X2L
Calculating:
1344.89=484+X2L
X2L=1344.89−484=860.89
XL=√860.89≈29.35Ω
To achieve a power factor of unity, we need:
XL=XC
Thus:
XC=29.35Ω
The capacitive reactance is given by:
XC=12πfC
Rearranging gives:
C=12πfXC
Substituting f=60Hz and XC=29.35Ω:
C=12π⋅60⋅29.35
Calculating:
C=12⋅3.14⋅60⋅29.35≈12⋅3.14⋅1761≈111079.48≈9.03×10−5F=90.3μF
The capacitance of the series capacitor that will result in a power factor of unity is approximately:
C≈90.3μF
Similar Questions
An AC circuit drawing power from a source of angular frequency 50 rad s−1 has a power factor of 0.6. In this condition, a resistance of 100Ω is present and the current is lagging behind the voltage. If a capacitor is connected in series, then the required capacitance that will result in a power factor of unity is
View SolutionThe power factor of the circuit in fig. is 1/√2. The capacitance of the circuit is equal to
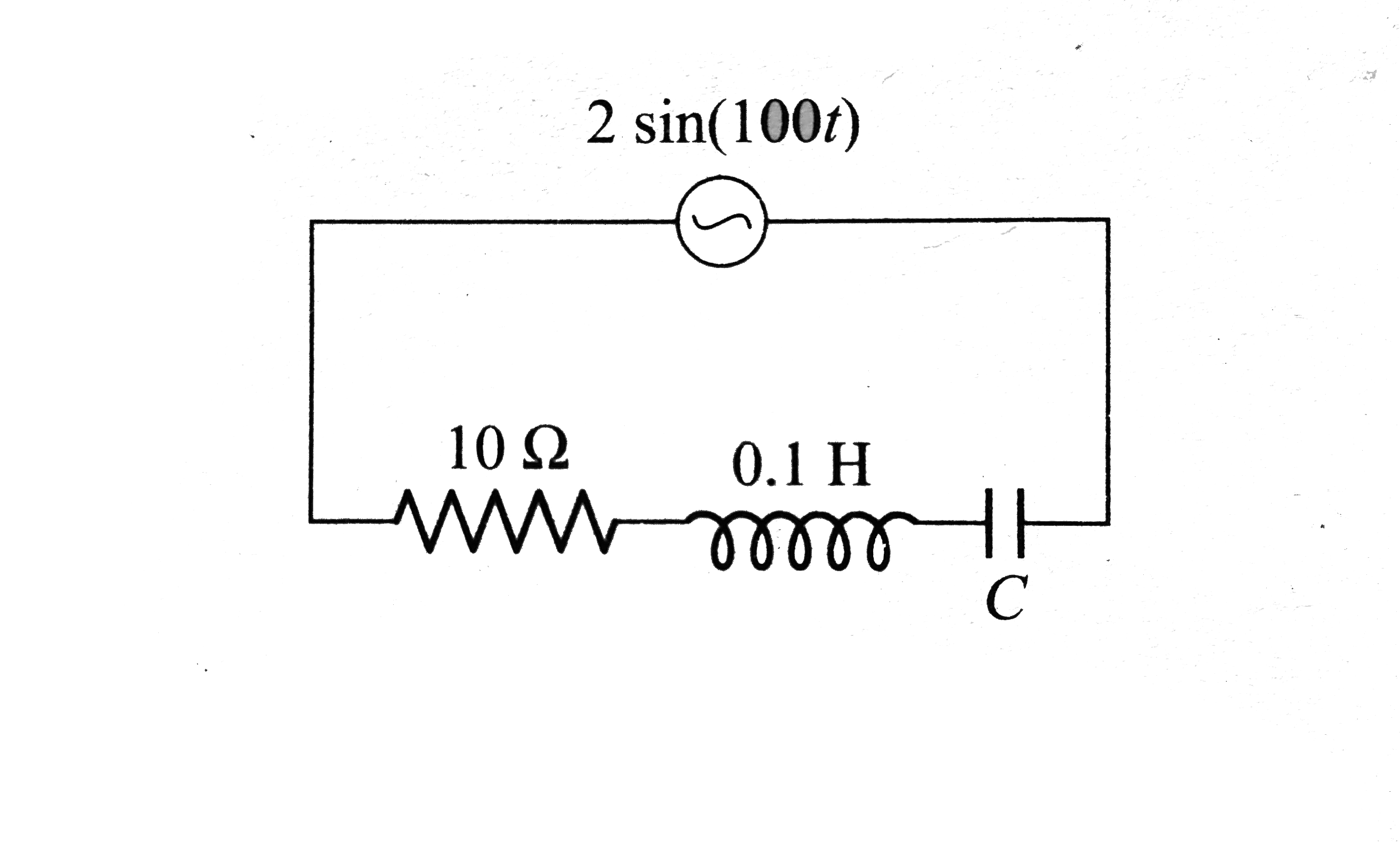 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A circuit draws a power of 550 watt from a source of 220 volt, 50Hz. The power factor of the circuit is 0.8 and the current lags in phase behind the potential difference. To make the power factor of the circuit as 1.0, The capacitance should be connected in series with it is
A142π×10−2FB141π×10−2FC15π×10−2FD184π×10−2F
An inductive circuit draws a power 550 W from a 220V-50Hz source. The power factor of the circuit is 0.8. The current in the circuit lags behind the voltage. Show that a capacitor of about 142π×10−2F will have to be commected in the circuit to bring its power factor to unity.
View SolutionIn the circuit shown in fin. Calculate the capacitance C of the capacitor, if the power factor of the circuit is unity. Also, calculate Q factor of the circuit.
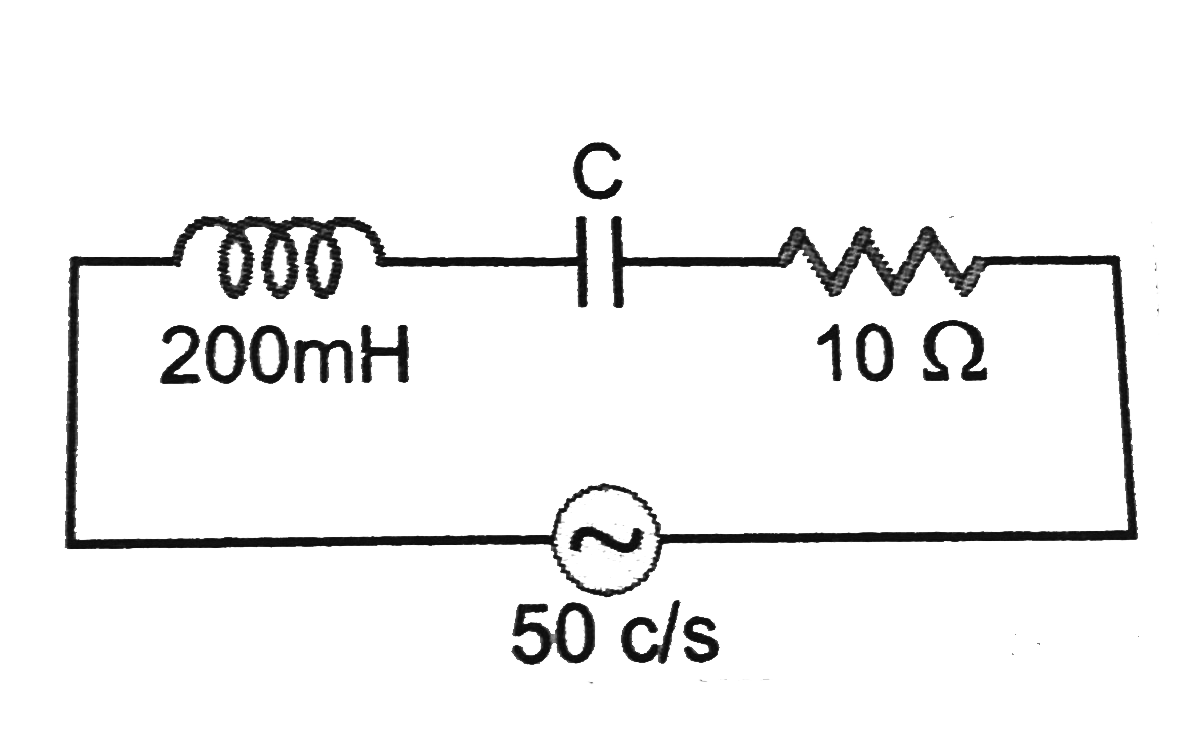 View Solution
View SolutionA circuit shown in the figure contains a box having either a capacitor or an inductor. The power factor of the circuit is 0.8, while current lags behind the voltage. Then find the inductance/capacitance of the box is S.I. unit (take π=3.2). The circuit draws 1 ampere current.
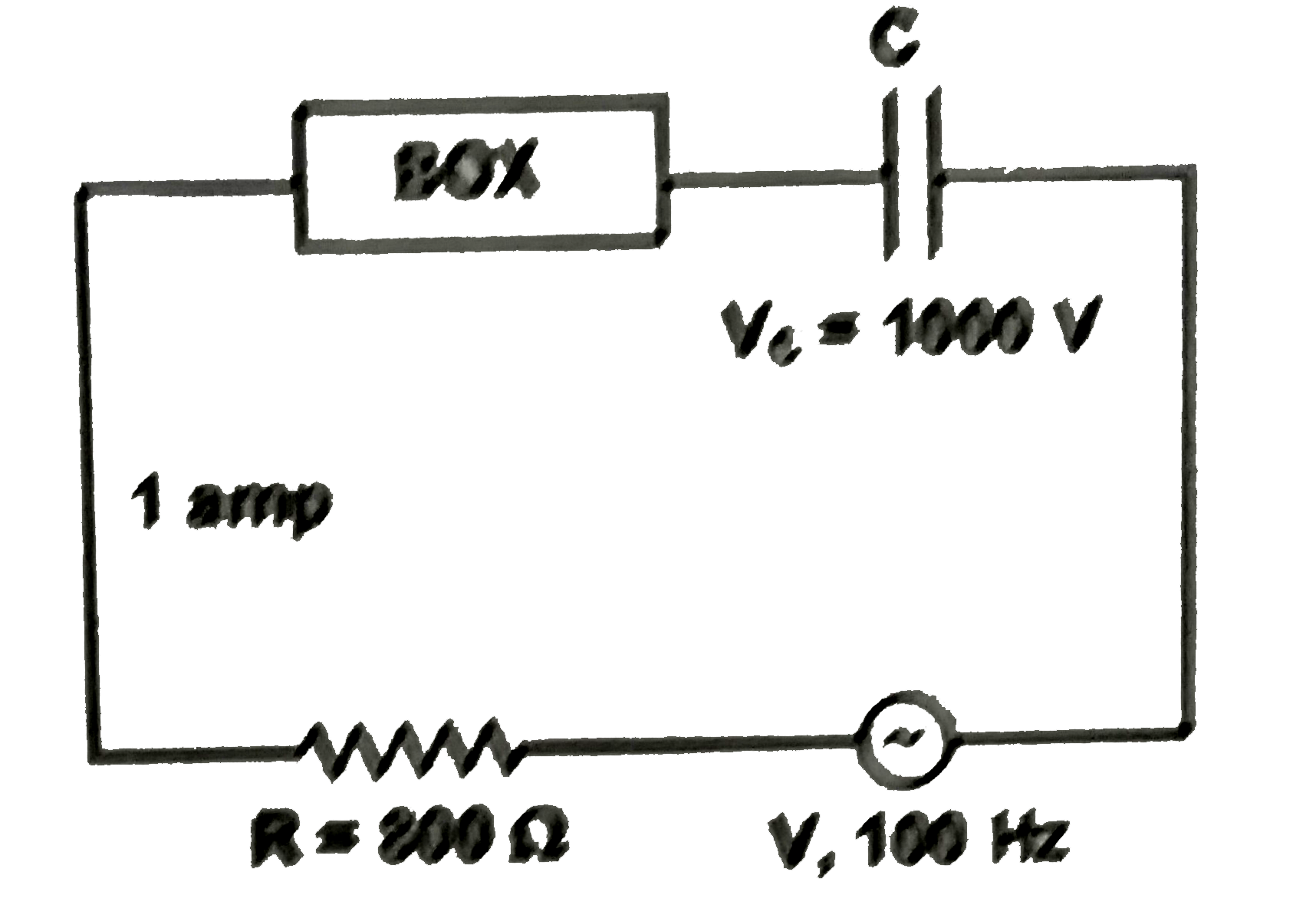 View Solution
View SolutionA 60μF capacitor is connected to a 110V, 60 Hz AC supply determine the rms value of the curent in the circuit.
View SolutionIn a series L.R circuit, power of 400 W is dissipated from a source of 250 V, 50 Hz. The power factor of the circuit is 0.8. In order to bring the power factor to unity, a capactor of value C is added in series to the L and R. Taking the value of C as (n3π)μF, then value of n is ____________
View SolutionA circuit element shown in the figureure as a box is having either a capacitor or an inductor. The power factor of the circuit is 0.8, while current lags behind the voltage. Find

(a) the source voltage V,
(b) the nature of the element in box and find its value.View SolutionAn L-R circuit has R = 10 Ω and L = 2H . If 120 V , 60 Hz AC voltage is applied, then current in the circuit will be
View Solution

