The refracting angle of a prism is A and refractive index of the material of prism is cot(A/2) . The angle of minimum deviation will be
To find the angle of minimum deviation (Δ_min) for a prism with a refracting angle A and a refractive index (μ) of cot(A/2), we can follow these steps:
1. Understand the relationship between refractive index and angles:
The refractive index of a prism at minimum deviation is given by the formula:
μ=sin(A+Δmin2)sin(A2)
2. Substitute the given refractive index:
We know that the refractive index μ is given as:
μ=cot(A2)
We can express cotangent in terms of sine and cosine:
cot(A2)=cos(A2)sin(A2)
3. Set the two expressions for μ equal:
Now, we equate the two expressions for the refractive index:
sin(A+Δmin2)sin(A2)=cos(A2)sin(A2)
4. Simplify the equation:
Since sin(A2) is present in both the numerator and denominator, we can cancel it out (assuming sin(A2)≠0):
sin(A+Δmin2)=cos(A2)
5. Use the identity for cosine:
We can rewrite cos(A2) using the sine identity:
cos(A2)=sin(90∘−A2)
6. Set up the equation:
Now we have:
sin(A+Δmin2)=sin(90∘−A2)
7. Solve for Δ_min:
Since the sine function is equal, we can set their arguments equal to each other:
A+Δmin2=90∘−A2
Multiplying through by 2 gives:
A+Δmin=180∘−A
Rearranging this gives:
Δmin=180∘−2A
Final Answer:
The angle of minimum deviation (Δ_min) is:
Δmin=180∘−2A
The refractive index of a prism at minimum deviation is given by the formula:
μ=sin(A+Δmin2)sin(A2)
We know that the refractive index μ is given as:
μ=cot(A2)
We can express cotangent in terms of sine and cosine:
cot(A2)=cos(A2)sin(A2)
Now, we equate the two expressions for the refractive index:
sin(A+Δmin2)sin(A2)=cos(A2)sin(A2)
Since sin(A2) is present in both the numerator and denominator, we can cancel it out (assuming sin(A2)≠0):
sin(A+Δmin2)=cos(A2)
We can rewrite cos(A2) using the sine identity:
cos(A2)=sin(90∘−A2)
Now we have:
sin(A+Δmin2)=sin(90∘−A2)
Since the sine function is equal, we can set their arguments equal to each other:
A+Δmin2=90∘−A2
Multiplying through by 2 gives:
A+Δmin=180∘−A
Rearranging this gives:
Δmin=180∘−2A
The angle of minimum deviation (Δ_min) is:
Δmin=180∘−2A
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.110videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.210videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
Similar Questions
The refracting angle of a prism is A, and refractive index of the material of the prism is cot(A2). The angle of minimum deviation is
View SolutionThe refractive index of the material of prism √3, then the angle of minimum deviation of prism is
View SolutionThe refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
View SolutionA ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the material of prism is 3^1/2, then the angle of deviation of the ray is
 View Solution
View SolutionWhen light rays are incident on a prism at an angle of 45∘, the minimum deviation is obtained. If refractive index of the material of prism is √2, then the angle of prism will be
View SolutionThe correct relation between the refractive index (μ) of the material of prism (A) and angle of minimum deviation (δ) is
View SolutionA certain prism of refracting angle 60∘ and of refractive index 2 is immersed in a liquid of refractive index √2 then the angle of minimum deviation will be
View SolutionIn an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
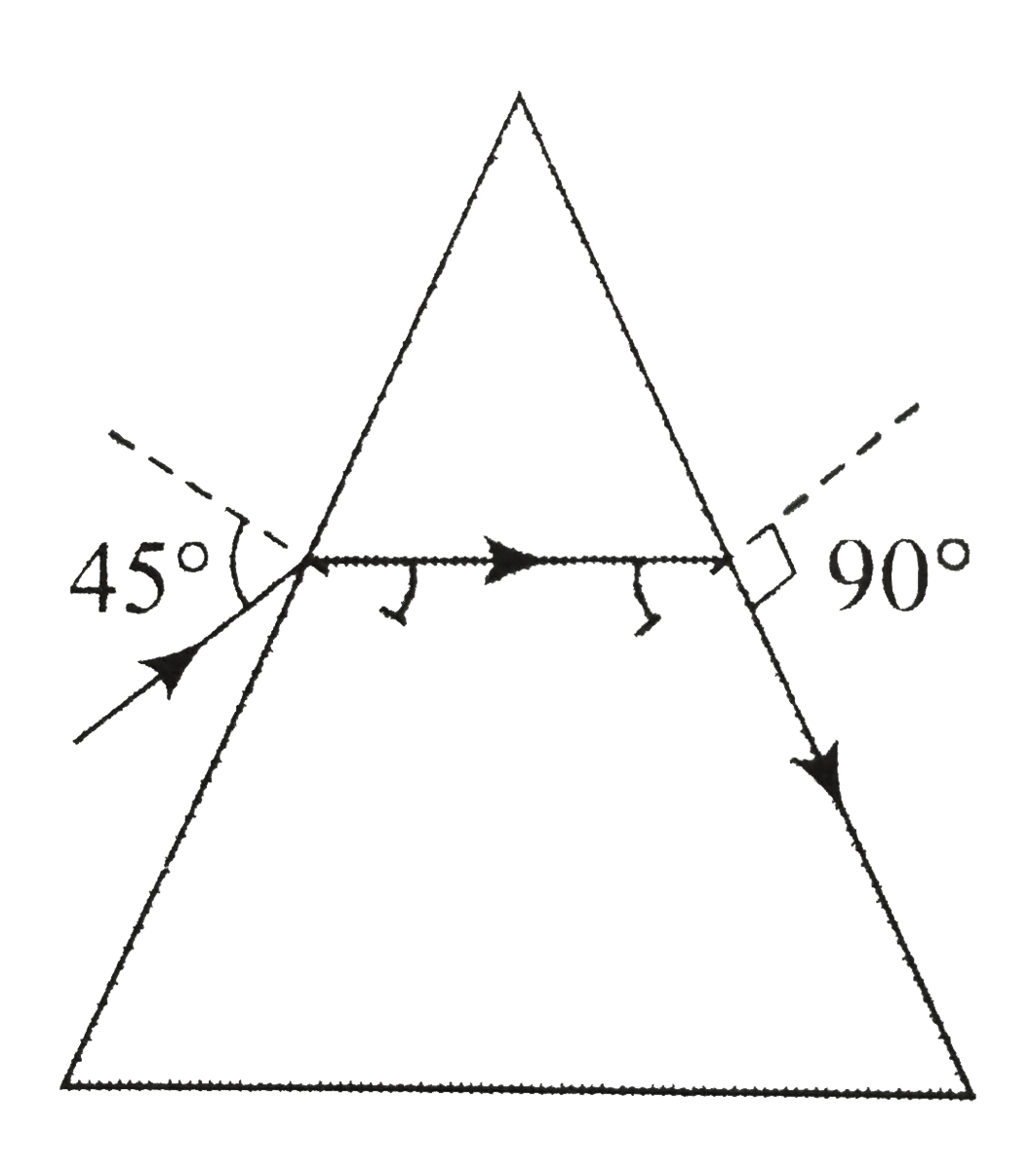 View Solution
View SolutionA prism is made up of material of refractive index √3. The angle of prism is A. If the angle of minimum deviation is equal to the angle of the prism, then the value of A is
View Solution(a) Plot a graph for angle of deviation as a function of angle of incidence for a triangular prism.
(b) Derive the relation for the refractive index of the prism in terms of the angle of minimum deviation and angle of prism.View Solution

