Speed (Vn) of electron in nth orbit versus principal quantum number (n) graphs is

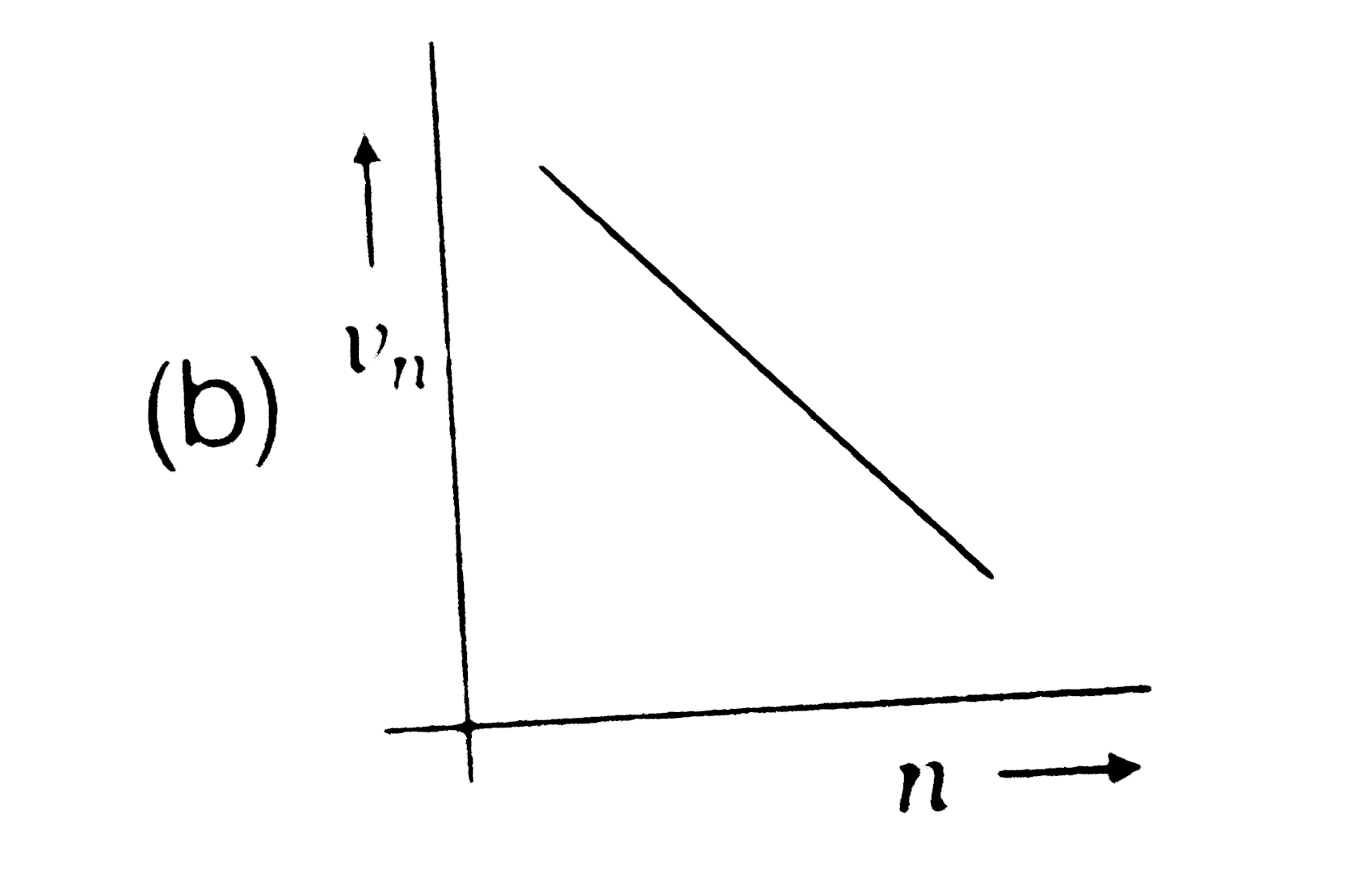
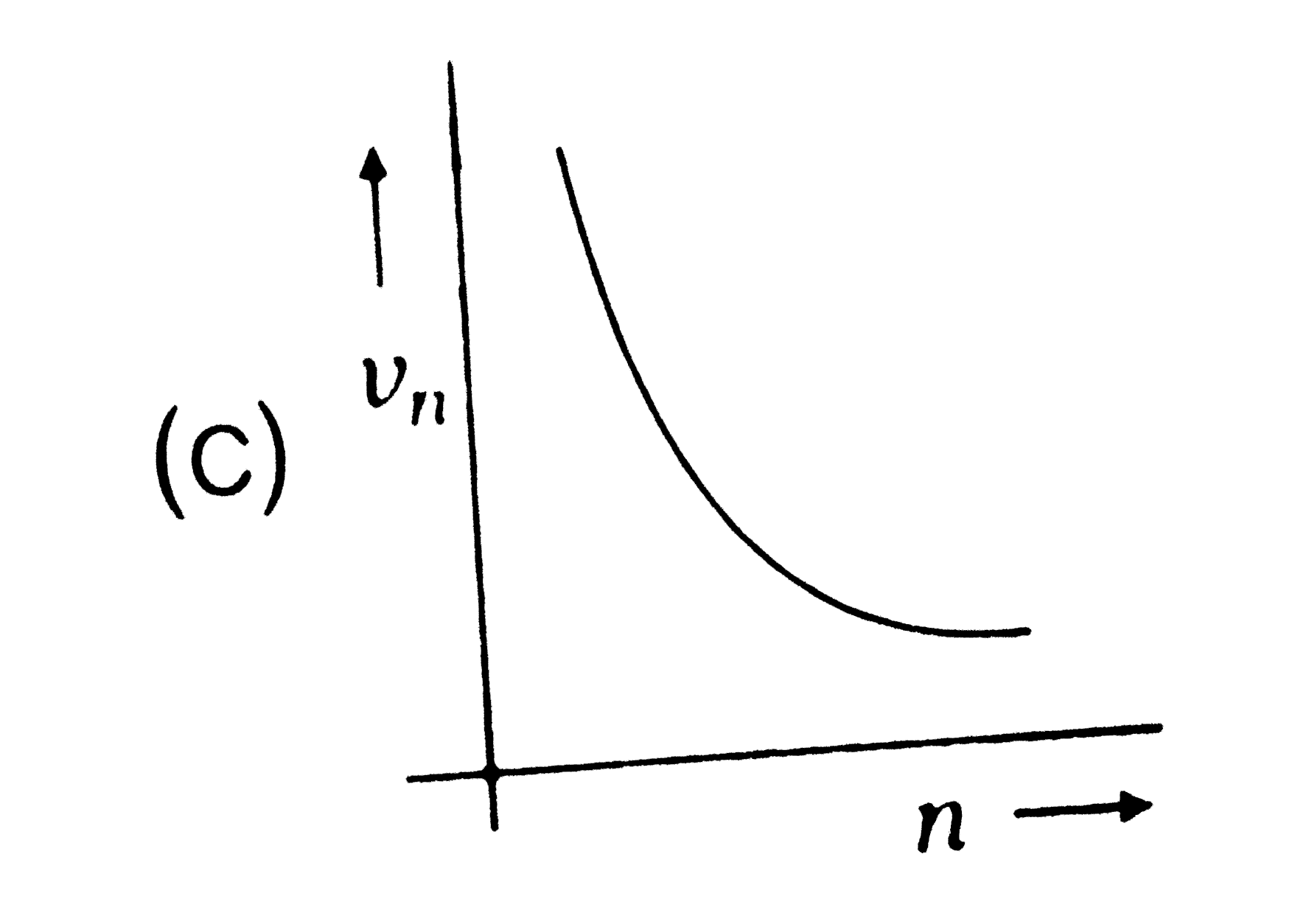

The correct Answer is:B
To solve the question regarding the speed Vn of an electron in the nth orbit versus the principal quantum number n, we can follow these steps:
1. Understand the Relationship:
The speed of an electron in the nth orbit is given by the formula:
Vn∝Zn
where Z is the atomic number of the element. For a given atom, Z remains constant.
2. Express the Relationship Mathematically:
Since Z is constant, we can simplify the relationship to:
Vn∝1n
This indicates that the speed Vn is inversely proportional to the principal quantum number n.
3. Graphical Representation:
When two quantities are inversely proportional, the graph of one quantity versus the other will be a hyperbola. Specifically, if we plot Vn on the y-axis and n on the x-axis, the graph will decrease as n increases.
4. Sketch the Graph:
- As n increases, Vn decreases.
- The graph starts from a higher value of Vn when n=1 and approaches zero as n increases indefinitely.
5. Identify the Correct Option:
Based on the graphical representation of the relationship Vn∝1n, we can conclude that the correct option for the graph of Vn versus n is the one that shows a hyperbolic decline.
Conclusion:
The correct graph for the speed Vn of an electron in the nth orbit versus the principal quantum number n is a hyperbola that decreases as n increases.
The speed of an electron in the nth orbit is given by the formula:
Vn∝Zn
where Z is the atomic number of the element. For a given atom, Z remains constant.
Since Z is constant, we can simplify the relationship to:
Vn∝1n
This indicates that the speed Vn is inversely proportional to the principal quantum number n.
When two quantities are inversely proportional, the graph of one quantity versus the other will be a hyperbola. Specifically, if we plot Vn on the y-axis and n on the x-axis, the graph will decrease as n increases.
- As n increases, Vn decreases.
- The graph starts from a higher value of Vn when n=1 and approaches zero as n increases indefinitely.
Based on the graphical representation of the relationship Vn∝1n, we can conclude that the correct option for the graph of Vn versus n is the one that shows a hyperbolic decline.
The correct graph for the speed Vn of an electron in the nth orbit versus the principal quantum number n is a hyperbola that decreases as n increases.
Topper's Solved these Questions
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - Check point 12.2
16 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - Check point 12.3
15 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
62 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
Similar Questions
Radius (rn) of electron in nth orbit versus atomic number (Z) graph is
View SolutionThe principal quantum number, n describes
View SolutionPrincipal quantum number is related to
View SolutionThe principal quantum number representwsw
View SolutionSupose the potential energy between electron and porton a distance r is given by U=−Ke23r3 Assuming Bohar's Model to be valid for this atom if the speed of elctron in nth orbit depends on the prinicpal quantum number n as v ∞nx then find the vlaue of x.
View Solutionthe number of electrons accommodated in an orbital with principal quantum number 3 is
View SolutionMaximum number of electrons in given shell identified by the principal quantum number n is equal to
View SolutionIn Bohr model of hydrogen atom, the force on the electron depends on the principal quantum number (n) as
View SolutionThe maximum number of electrons that can have principal quantum number, n = 3, and spin quantum number ms = - 1 /2, is
View SolutionAccording to Bohr's theory, the time averaged magnetic field at the centre (i.e. nucleus) of a hydrogen atom due to the motion of electrons in the nth orbit is proportional to :
(n = principal quantum number)
View Solution
