A long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

μ0I4r
μ0I24r
μ0I4r2
None of these
The correct Answer is:A
According to Biot savart Law, the magnetic induction at a point to a current carrying elemnet i δ l is given by
δB=μ04π<al×rr3orB=μ04π<alsinθr2
Directed normal to plane containing δl and
r theta being angle between δl and r
r θ being angle between δ l and r
Magnetic field due to linear portions of wire
If we consider anuy element of lenth δl of either linear portion ab or de, the angle between δ l and r is 0 or π therefore.
sinθ=0
Hence, magnetic induction due to both linear portins of wire is
μ04π<alsinθr=0
Field due to semi circular are
Now angle between a current element δ l of semi circular arc and the radius vector of the elment to point c is π/2
Therefoe the magnitude of magnetic induction B at O due to this element is
δB=μ04π<alsinπ/2r2=μ0<al4πr2
Hence magnetic indution due to whole semi circular loop is B=Σμ04π<alr2=μ04πr2=μ04πii2Σδi=μ0i4πR2(πr)=μ0i4r
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)32videos
SOLVED PAPER 2017
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)32videos
SOLVED PAPER 2017
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER22videos
SOLVED PAPERS 2018
Similar Questions
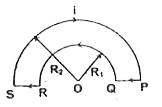
The wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
 View Solution
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.
 View Solution
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
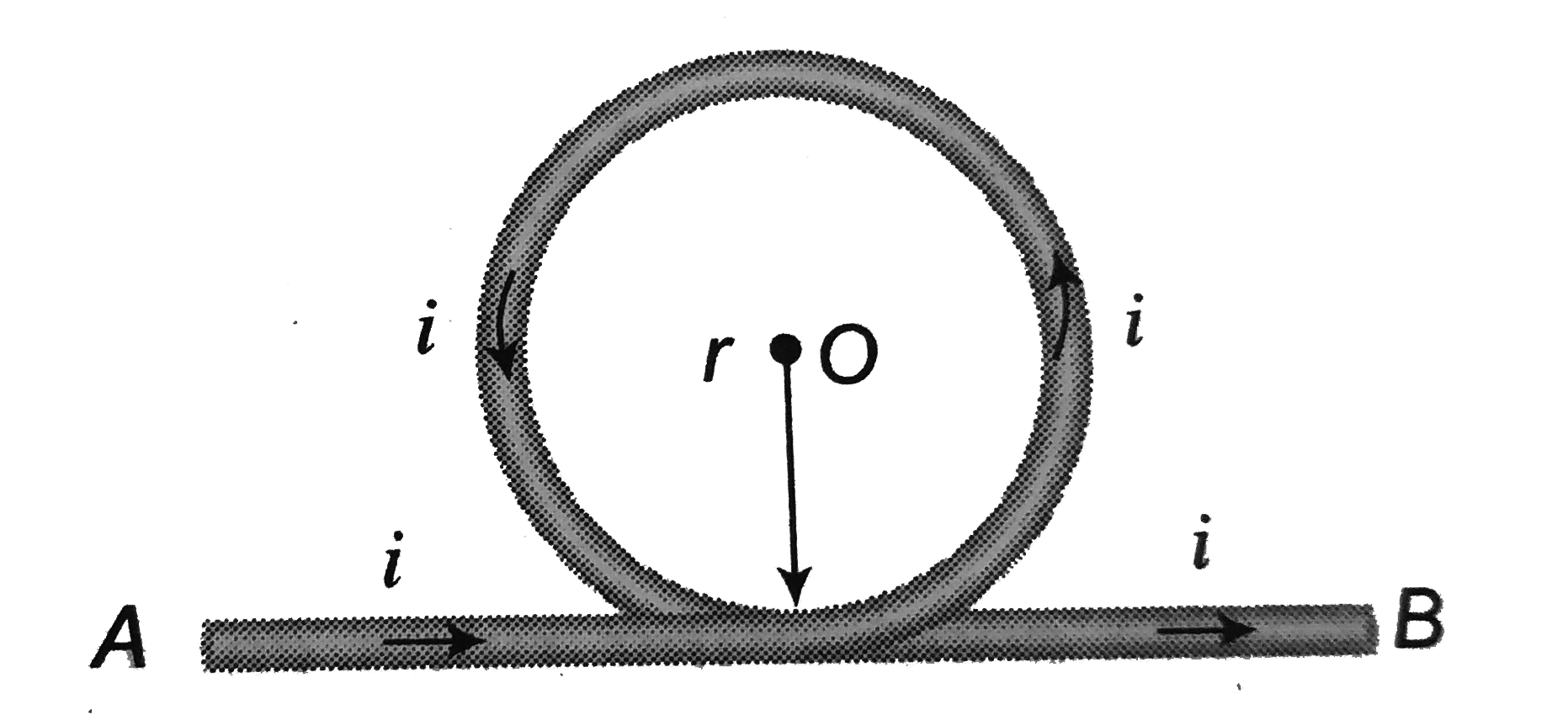 View Solution
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :
 View Solution
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop
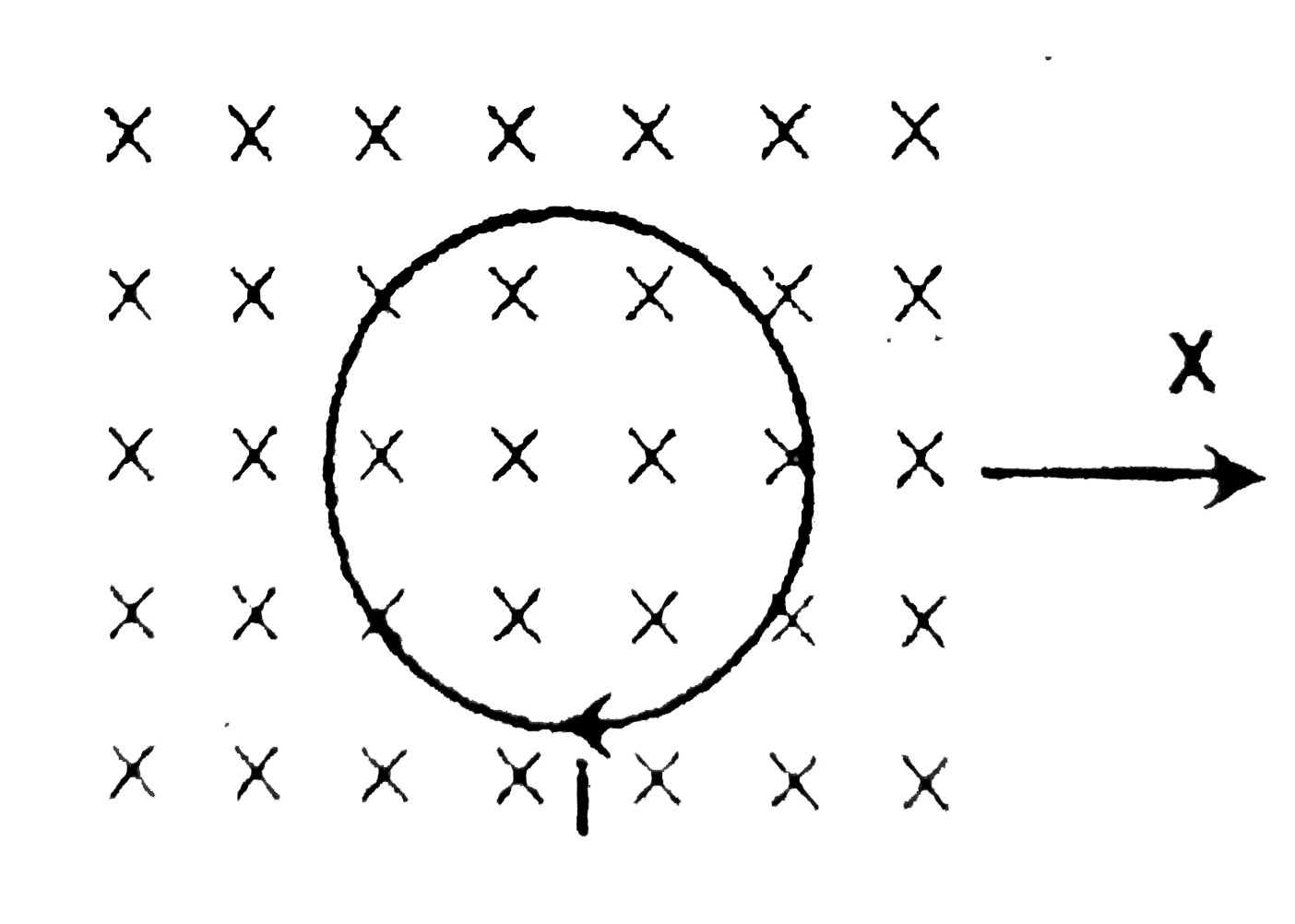 View Solution
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.
 View Solution
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is
 View Solution
View SolutionTwo very long, straight wires carrying, currents as shown in Fig. Find all locations where the net magnetic field is zero.
 View Solution
View SolutionA small circular flexible loop of wire of radius r carries a current I. It is placed in a uniform magnetic field B. The tension in the loop will be doubled if (Choose the incorrect option)
View Solution

