An electric dipole is a pair of equal and opposite point charge +q and -q separated by a distance r.Write an expresion for its dipole moment.
p=q×r
Similar Questions
A pair of equal and opposite point charge "+q" and "-q separated by small distance "2a is called
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector →p of an electric dipole as →p=q(2a) and its direction is along the line from q to + q charge. The dipole field at large distances fall off as 1r3. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector →r and the dipole moment →p.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
In which direction is the magnitude of electric field due to a short dipole (i) maximum, (ii) minimum ? Write expression for the same.
View Solution
Knowledge Check
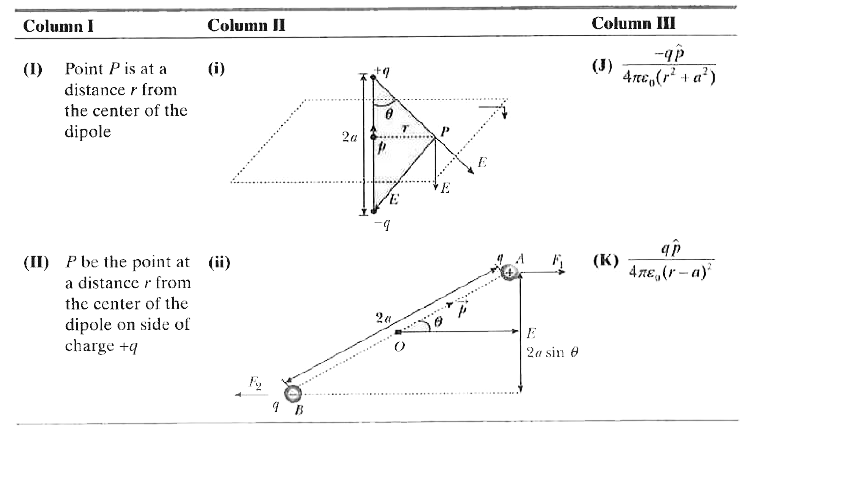
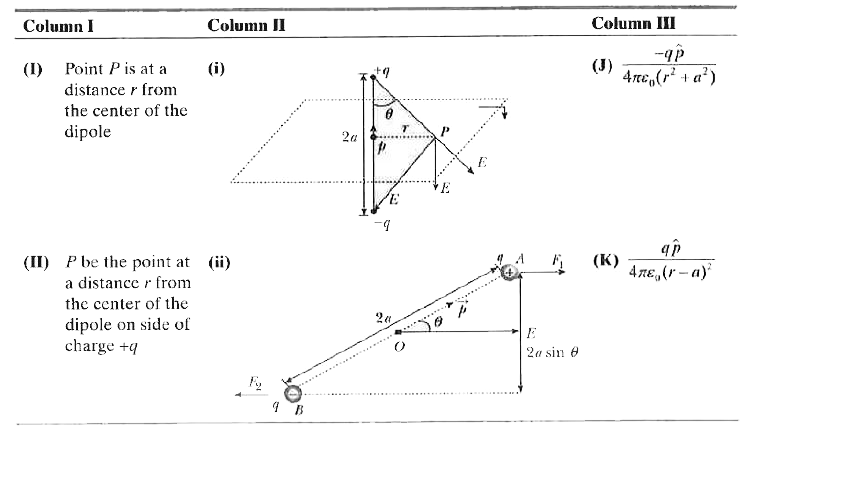
An electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
When point P lies on the equatorial plan of the electric dipole, electric field due to -q is ?
 A(I) (i) (J)B(I) (i) (M)C(III)(iii) (J)D(I) (i) (K)
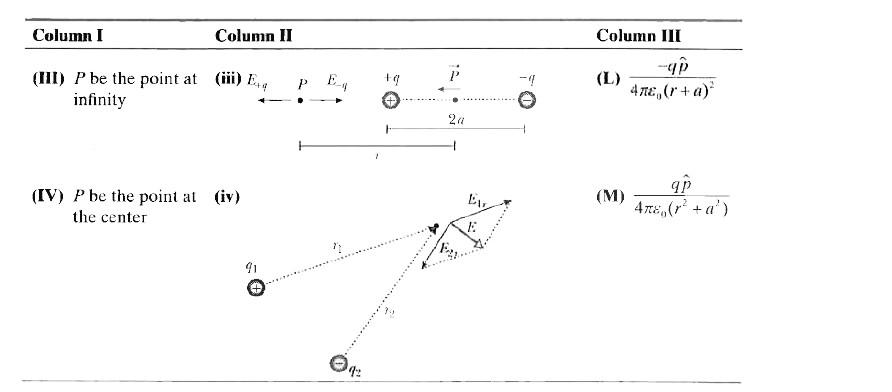
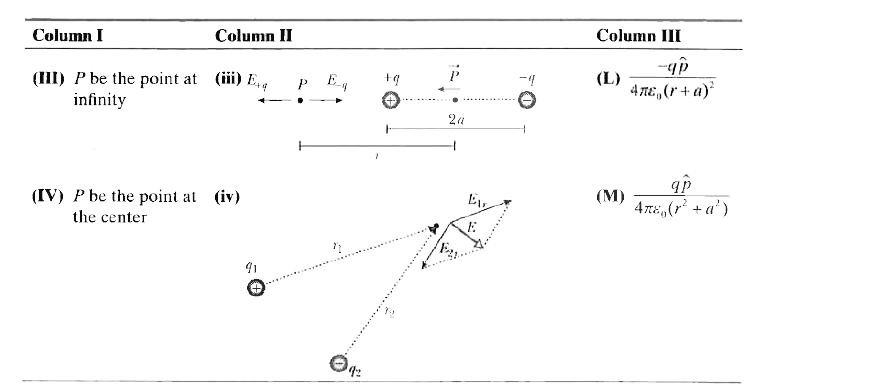
A(I) (i) (J)B(I) (i) (M)C(III)(iii) (J)D(I) (i) (K)An electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
when point P lies on the equatorial plane of the electric dipole, electric field due to +q is ?
 A(III) (ii) (L)B(IV) (i) (M)C(III) (iii) (J)D(I) (i) (M)
A(III) (ii) (L)B(IV) (i) (M)C(III) (iii) (J)D(I) (i) (M)An electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
When point P lies on the axis of the electric dipole, electric field due to -q is ?

 A(III) (ii) (L)B(II) (iii) (L)C(II) (iii) (J)D(I) (i) (K)
A(III) (ii) (L)B(II) (iii) (L)C(II) (iii) (J)D(I) (i) (K)
On the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector →p of an electric dipole as →p=q(2a) and its direction is along the line from q to + q charge. The dipole field at large distances fall off as 1r3. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector →r and the dipole moment →p.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
Is the electric field due to a charge configuration with total charge zero necessarily zero ? Give an illustration in support of your answer.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector →p of an electric dipole as →p=q(2a) and its direction is along the line from q to + q charge. The dipole field at large distances fall off as 1r3. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector →r and the dipole moment →p.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
Define polarisation vector and give its SI unit.
View SolutionAn electric dipole of dipole moment →p consists of point charges + q and - q separated by a distance 2a apart. Deduce the expression for the electric field →E due to the dipole at a distance x from the center of dipole on its axial line in terms of the dipole moment →p . Hence show that in the limit a→0→E=2→p(4πε0x3).
View SolutionAn electric dipole of dipole moment →p consists of point charges +q and -q separated by a distance '2a' apart. Deduce the expression for the electric field →E due to the dipole on its axial line in term of the dipole moment →p. Hence show that in the limit r>>a,→E=2→p4π∈0r3
(b) Given the electric field in the region →E=2xˆi Find the net electric flux through the cube and the charge enclosed by it.
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign separately by a distance 2a. The dipole is along the X-axis and is centred at the origin
(i) Calculate the electric potential at point P
(ii) Calculate V at a point far from the dipole.
View Solution
