According to newton’s low of motion, the force depends on the rate of change of r momentum A man jumping out of a moving bus falls with his head forward. What should he do in order to long safety ?
He should run for some distance in the direction of motion of the bus
Similar Questions
a. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?

View Solutiona. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?

View Solution
Knowledge Check
According to Newton s second law of motion F=ma where F is the force required to produce an acceleration a in a body of mass m If a = 0 then F=0 no external force is required to move a body uniformly along a straight line If a force F acts on a body for t seconds the effect of the force is given by Impulse =F × t =change in linear momentum of the body
Average force exerted by the bat is .A480NB120NC1200ND840NAccording to Newton s second law of motion F=ma where F is the force required to produce an acceleration a in a body of mass m If a = 0 then F=0 no external force is required to move a body uniformly along a straight line If a force F acts on a body for t seconds the effect of the force is given by Impulse =F × t = change in linear momentum of the body
The retardation of the ball is .A1600m/s2B320m/s2C3200m/s2D160m/s2According to Newton s second law of motion F=ma where F is the force required to produce an acceleration a in a body of mass m If a = 0 then F=0 no external force is required to move a body uniformly along a straight line If a force F acts on a body for t seconds the effect of the force is given by Impulse =F × t = change in linear momentum of the body
A cricket ball of mass 150g is moving with a velocity of 12m/s and is hit by a bat so that the ball is turned back with a velocity of 20m/s if duration of contact between the ball and the bat is 0.01sec The impulse of the force is .A7.4N−sB4.8N−sC1.2N−sD4.7N−s
The following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
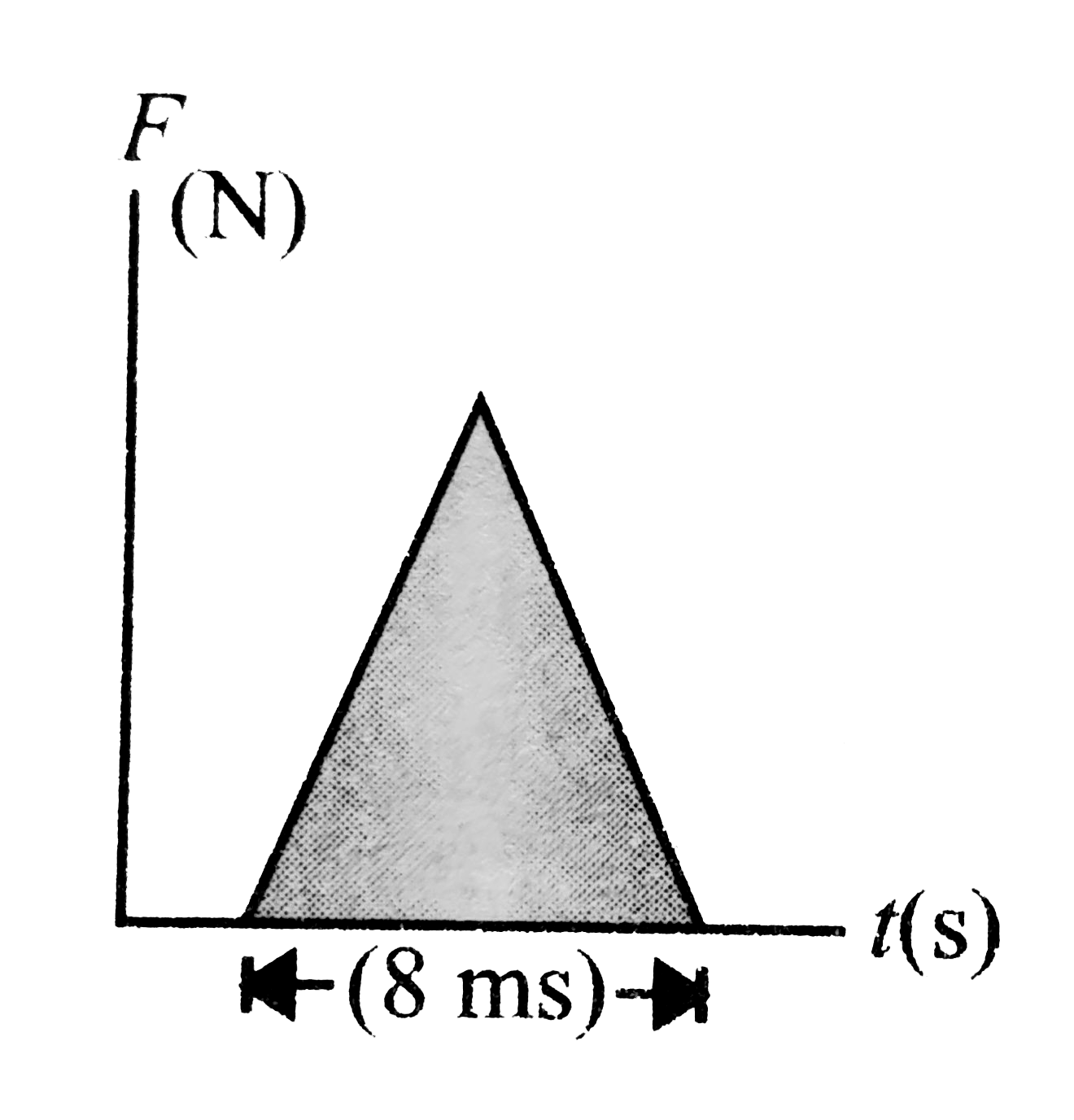
Maximum force exerted by the bat on the ball is
View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
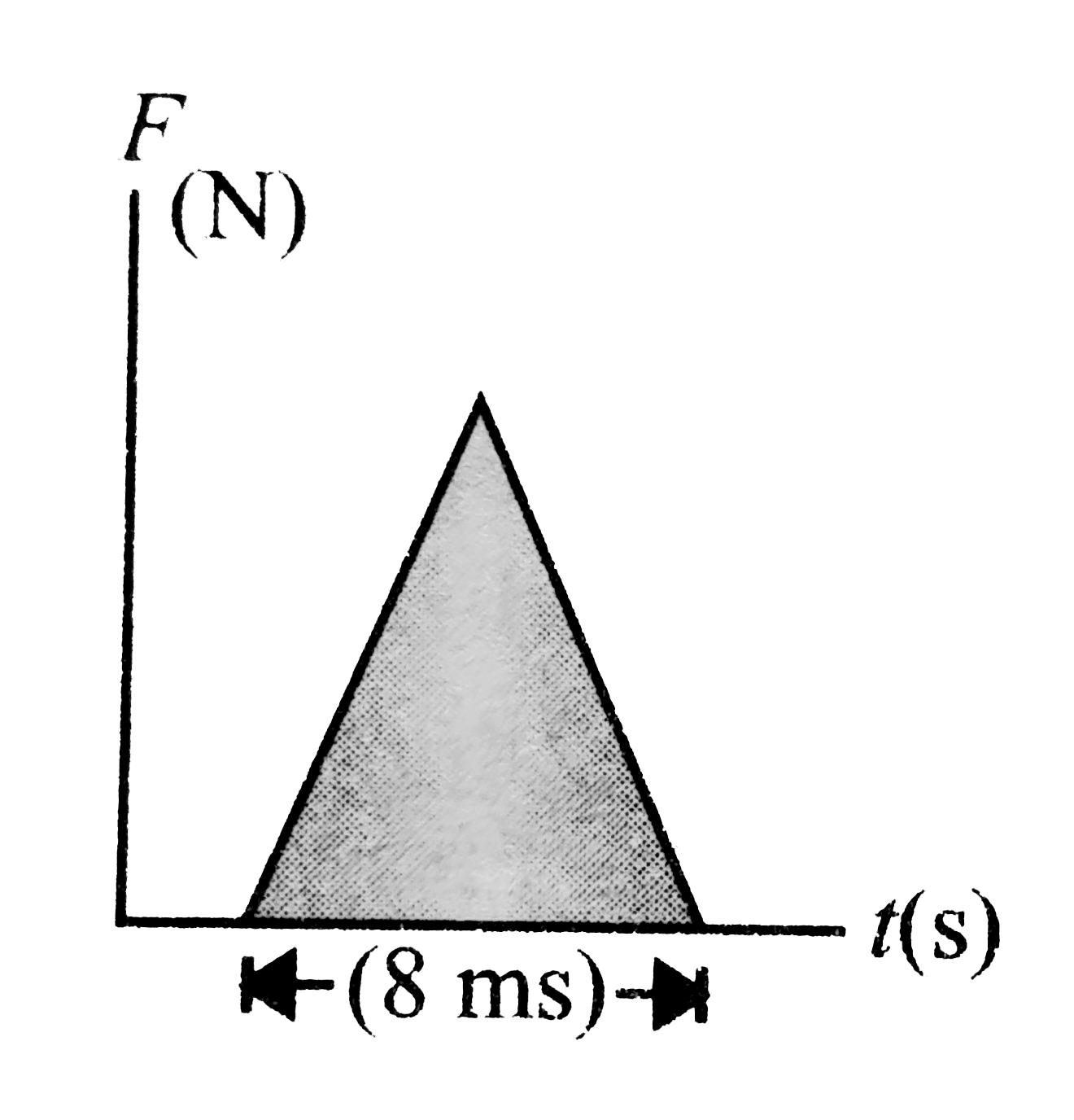
Linear momentum of the ball immediately after colliding with the floor will be
View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
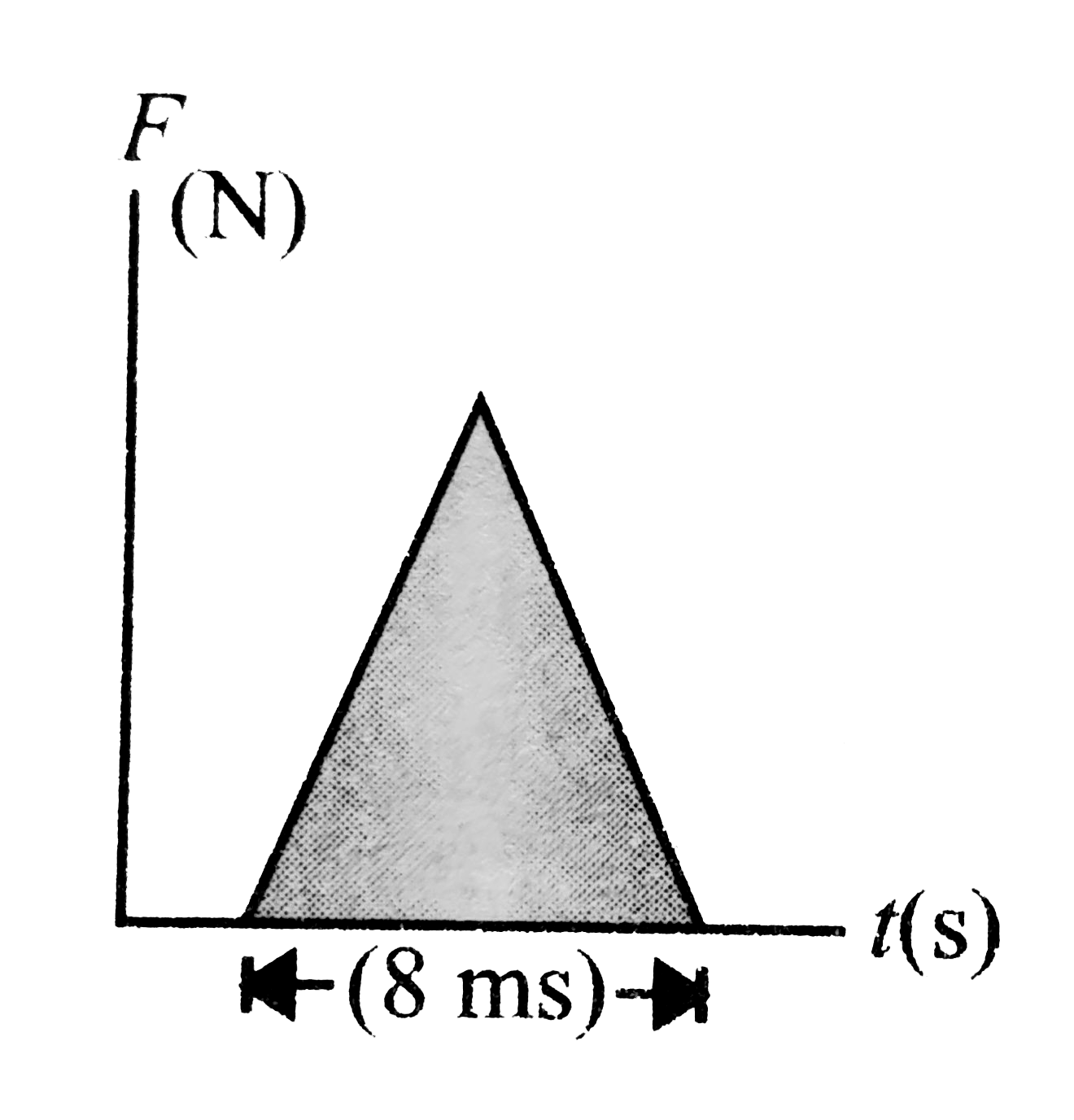
Maximum force exerted by the bat on the ball is
View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
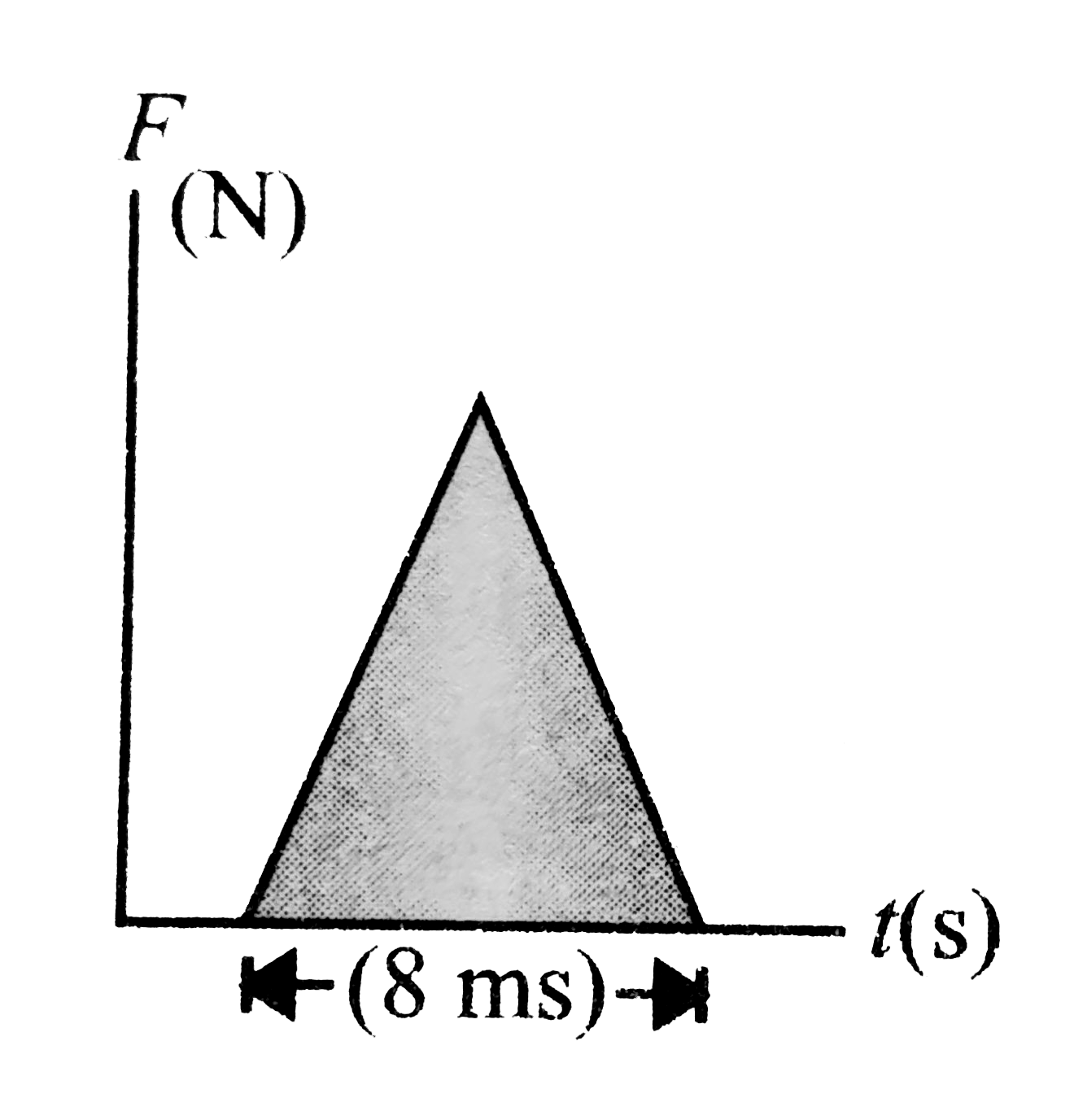 After collision with the hard floor, the ball will bounce to a height
After collision with the hard floor, the ball will bounce to a height
View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
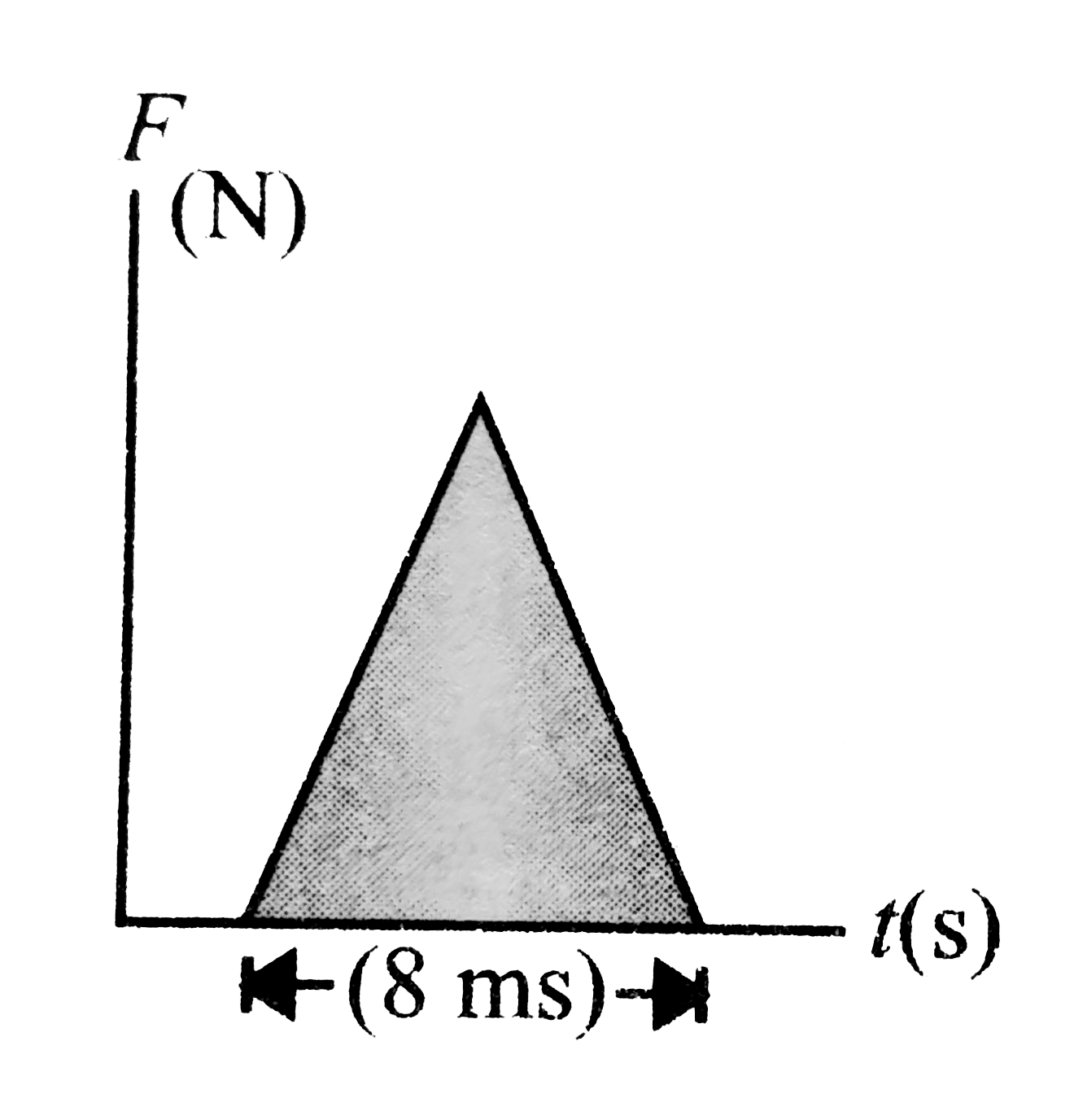
Average force exerted by the bat on the ball is
Let us consider another example. The given ball of mass 250g is dropped from a height 5m on a hard floor. Force exerted by the floor on the ball, as long as these are in contact, varies with time as shown in Fig.

View Solution
