यदि A−1=⎡⎢ ⎢⎣sin2α000sin2β000sin2γ⎤⎥ ⎥⎦ तथा B−1=⎡⎢⎣cos2α000cos2β000cos2γ⎤⎥⎦ है जहाँ α,β,γ वास्तविक संख्याएँ है तथा C=(A−3+B−3)+3A−1B−1(B−1+A−1) है , तो आव्यूह C के सारणिक का मान ज्ञात कीजिये।
The correct Answer is:1
Step by step video, text & image solution for यदि A^(-1)=[(sin^(2)alpha,0,0),(0,sin ^(2)beta,0),(0,0,sin^(2)gamma)] तथा B^(-1)=[(cos^(2)alpha,0,0),(0,cos^(2)beta,0),(0,0,cos^(2)gamma)] है जहाँ alpha,beta,gamma वास्तविक संख्याएँ है तथा C=(A^(-3)+B^(-3))+3A^(-1)B^(-1)(B^(-1)+A^(-1)) है , तो आव्यूह C के सारणिक का मान ज्ञात कीजिये। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSAL HINDICHAPTER - DETERMINANT & MATRICSEXERCISE - EXERCISE -3 SECTION -A (JEE-ADVANCED Previous Year.s Questions) (Determinants)6videos
DETERMINANT & MATRICS
- BOOK - BANSAL HINDICHAPTER - DETERMINANT & MATRICSEXERCISE - EXERCISE -3 SECTION -A (JEE-ADVANCED Previous Year.s Questions) (Matrics)25videos
DETERMINANT & MATRICS
- BOOK - BANSAL HINDICHAPTER - DETERMINANT & MATRICSEXERCISE - EXERCISE -2 SECTION -A [DETERMINANT]30videos
DETERMINANT & MATRICS
- BOOK - BANSAL HINDICHAPTER - CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)EXERCISE - EXERCISE - 518videos
CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)
- BOOK - BANSAL HINDICHAPTER - INDEFENITE & DEFINITE INTEGRATION EXERCISE - EXERCISE -5 ( Rank Booster)23videos
INDEFENITE & DEFINITE INTEGRATION
Similar Questions
माना तीन बिन्दु
P=(−sin(β−α),−cosβ),Q=(cos(β−α),sinβ) तथा R=(cos(β−α+θ),sin(β−θ)) है, जहाँ 0<α,β,θ<π405:39View Solutionस्तम्भ I में कथनों/व्यजनों को स्तम्भ-II में कथनों/व्यंजकों से मिलाईये तथा अपने OMR में दिए 4×4 आव्यूह में उचित गोले को कला करके निर्देशित कीजिये |
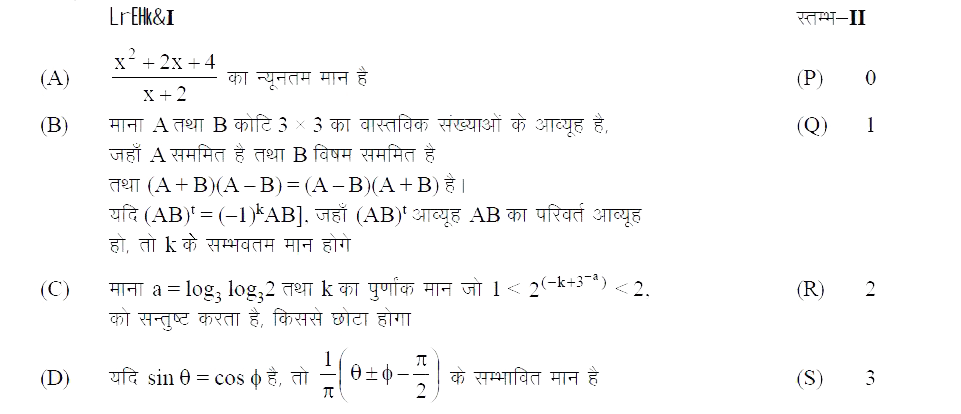03:05View Solutionसिद्ध कीजिये की सारणिक ∣∣ ∣ ∣∣−75+3i23−4i5−3i84+5i23+4i4−5i9∣∣ ∣ ∣∣ का मान वास्तविक है
10:39View Solutionबिन्दु P(h, k) से परवलय x2=8y पर तीन अभिलम्ब डाले गये है तथा m1,m2 तथा m3 इन तीनों की प्रवणताऐं है। इन तीनों अभिलम्बों की प्रवणताओं का बीजगणितीय योग ज्ञात कीजिए।
01:32View Solutionनिम्नलिखित समाकल का मान ज्ञात कीजिए-
∫sin−1√xa+xdx.01:53View SolutionIf A^(-1)=[(sin^2alpha,0,0),(0,sin^2 beta,0), (0,0,sin^2gamma)] and B^(-1)=[(cos^2alpha,0,0),(0,cos^2 beta,0), (0,0,cos^2gamma)] where alpha, beta, gamma are any real numbers and C=A^(-5)+B^(-5)+5A^(-1)B^(-1)(A^(-3) +B^(-3))+10 A^(-2)B^(-2)(A^(-1)+B^(-1)) then find |C|
05:09View SolutionIf (0,0) is orthocentre of triangle formed by A(cos alpha,sin alpha),B(cos beta,sin beta),C(cos gamma,sin gamma) then /_BAC is
05:31View SolutionIf cos alpha + cos beta + cos gamma = 0 = sin alpha + sin beta + sin gamma then (a) sin ^ (2) alpha + sin ^ (2) beta + sin ^ (2) gamma = (3) / ( 2) (b) sin ^ (2) alpha + sin ^ (2) beta + sin ^ (2) gamma = (3) / (4) (c) cos ^ (alpha) + cos ^ (2) beta + cos ^ (2) gamma = (3) / (2) (d) cos ^ (2) alpha + cos2 beta + cos2 gamma = -1
06:50View SolutionIf (0,0) is orthocentre of triangle formed by A(cos alpha,sin alpha),B(cos beta,sin beta),C(cos gamma,sin gamma) then /_BAC=
09:09View SolutionIf cos alpha+cos beta+cos gamma=0, where 0
08:52View SolutionIf A(α,β)=⎡⎢⎣cosαsinα0−sinαcosα000eβ⎤⎥⎦, then A(α,β)−1 is equal to
04:21View Solutionयदि cos(β−γ)+cos(γ−α)+cos(α−β)=−32, तो सिद्ध करें की cosα+cosβ+cosγ=0,sinα+sinθ+sinγ=0
04:48View Solutionसिद्ध करे कि
sin(β−γ)+sin(γ−α)+sin(α−β)
+4sin12(β−γ)sin12(γ−α)sin12(α−β)=005:16View SolutionA(α,β)=⎛⎜⎝cosαsinα0−sinαcosα000eβ⎞⎟⎠=[A(α,β)]−1=
05:20View SolutionIfcos(β−γ)+cos(γ−α)+cos(α−β)=−32,show that,
cosα+cosβ+cosγ=0andsinα+sinβ+sinγ=0.Hence deduce that,
cos(β−γ)=cos(γ−α)=cos(α−β)=−12.04:33View SolutionIf ∣∣ ∣ ∣∣1cosαcosβcosα1cosγcosβcosγ1∣∣ ∣ ∣∣=∣∣ ∣ ∣∣0cosαcosβcosα0cosγcosβcosγ0∣∣ ∣ ∣∣ then the value of cos2α+cos2β+cos2γ is :
View Solution