Calculate the packing efficiency in simple cubic unit cell.
Text Solution
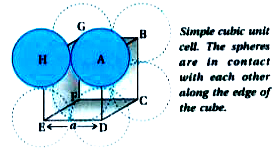
In a simple cubic unit cell, two spheres at the corners of the cube touch each other.
Let edge length of cube = a.
Let radius of sphere = r
The radius of sphere and edge length of cube is related as:
a = 2r
The volume of cubic unit cell =a3=(2r)3=8r3
Since the simple cubic unit cell contains only 1 atom, the volume of the occupied space is = 43πr3
% Packing efficiency = Volume occupied by four spheres in unit cell×100Volume of the unit cell
=43πr3_(8r3)×100=π6×100
52.4%.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - THE SOLID STATEEXERCISE - SECTION - A (EXAMPLES)5videos
THE SOLID STATE
- BOOK - KUMAR PRAKASHANCHAPTER - THE SOLID STATEEXERCISE - SECTION - B (INTEXT QUESTIONS AND ANSWERS)23videos
THE SOLID STATE
- BOOK - KUMAR PRAKASHANCHAPTER - THE SOLID STATEEXERCISE - SECTION - E (MULTIPLE CHOICE QUESTIONS)(MCQs ASKED IN BOARD EXAMS)35videos
THE SOLID STATE
- BOOK - KUMAR PRAKASHANCHAPTER - THE P-BLOCK ELEMENTS EXERCISE - SECTION-E (MULTIPLE CHOICE QUESTIONS (MCQS)) (MCQS ASKED IN BOARD EXAM)77videos
THE P-BLOCK ELEMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
Assertion (A) : Packing efficiency in simple cubic unit cell is 52.4%.
Reason (R) : Density of the unit cell is given by the relation : d=a3NAZM.ABoth Assertion (A) and Reason (R) are correct statements, and Reason (R) is the correct explanation of the Assertion (A).BBoth Assertion (A) and Reason (R) are correct statements, but Reason (R) is not the correct explanation of the Assertion (A).CAssertion (A) is correct, but Reason (R) is incorrect statement.DAssertion (A) is incorrect, but Reason (R) is correct statement. - Question 2 - Select One
The efficiency of packing in simple cubic unit cell is
Aπ6B√3π8C√2π6Dπ16 - Question 3 - Select One
The efficiency of packing in simple cubic unit cell is
Aπ6B√3π8C√2π6Dπ16
The efficiency of packing in simple cubic unit cell is
View SolutionThe packing fraction of a simple unit cell is ________.
View SolutionAssuming that atoms are touching each other, calculate the packing efficiency in case of a crystal of simple cubic metal.
View SolutionThe Packing efficiency in unit cell is
View SolutionThe packing fraction of the primitive cubic unit cell is
View Solution
