Doubtnut Promotions Sticky

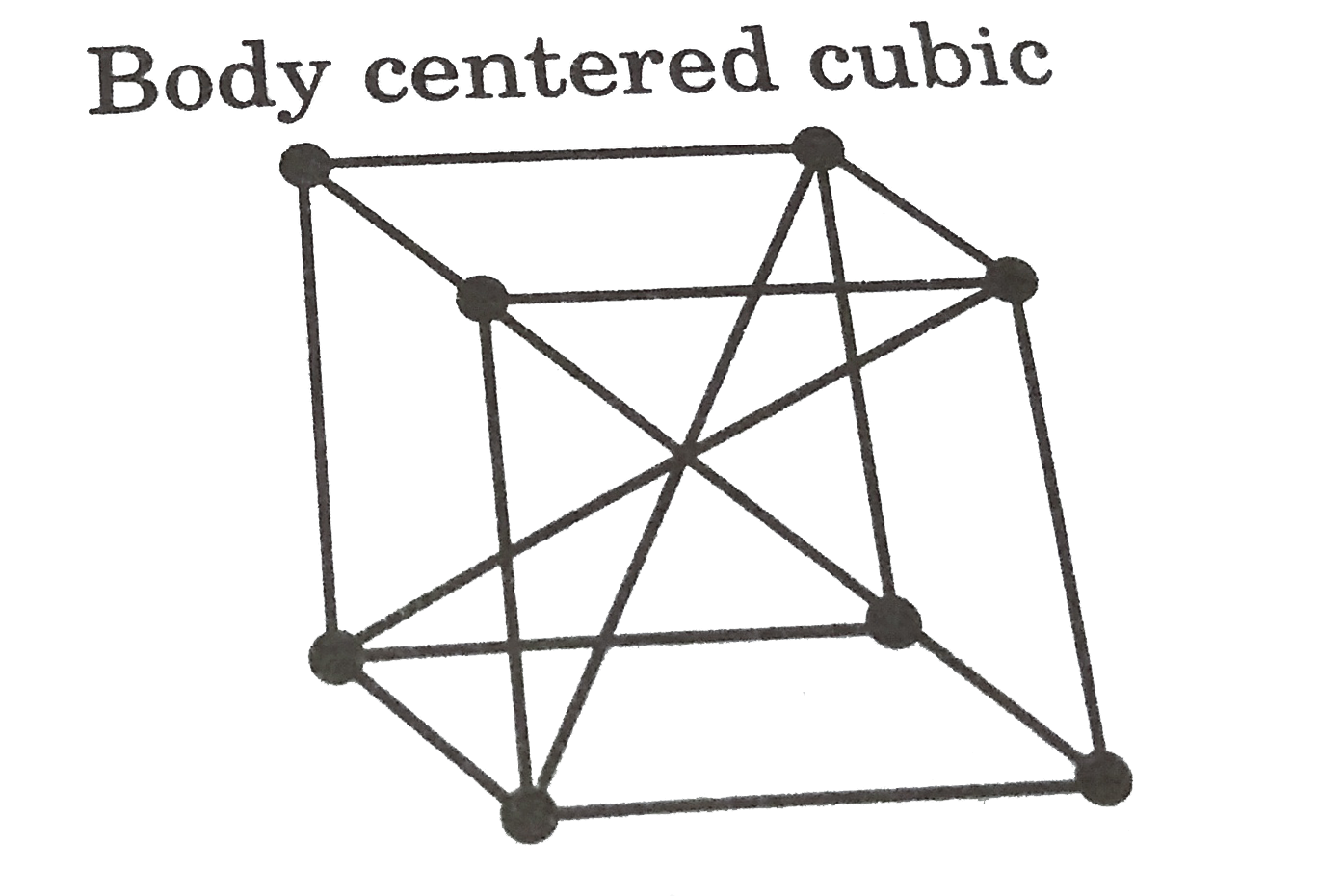
Explain how much portion of an atom located at (i) corner and (ii) body-centre of a cubic unit cell is part of its neighbouring unit cell. 

Text Solution
Verified by Experts

(i) The atom located at the corner of a cubic unit cell is shared by eight neighbouring unit cells.  
 Hence, it shares (18)th a portion of an atom.
(ii) The atom located at body-centred shares no portion of it with any neighbouring unit cell. It belongs fully to only one unit cell.

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12CHEMISTRYSOLID STATE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    How much prtion of an atom located at coner and at body centred of a cubic unit cell?

    A1,12
    B12,1
    C18,1
    D18,12
  • Question 2 - Select One

    The coordination number of each atom in body centered cubic unit cell is

    A(0,0,0) and (1/2,0,0)
    B(0,0,0) and (1/2,1/2, 1/2)
    C(0,0,0) and (0,1/2,0)
    D(0,0,0) and (0,0,1/2)