Question

R त्रिज्या की पतली वलय को x-y तल में इस प्रकार रखा जाता है कि इसका केन्द्र मूलबिन्दु पर रहता है। $x<0$ क्षेत्र वाली आधी वलय पर $+\lambda C/m$ समरूप रेखिय आवेश घनत्व है तथा शेष आधी वलय पर ($x>0$ क्षेत्र में) $-\lambda C/m$ समरूप रेखिय आवेश घनत्व है।

Options

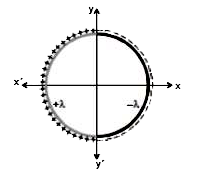
A. तब बिन्दू P जिसके निर्देशांक `(0m, +(R )/(2)m)` है पर विद्युत क्षेत्र की दिशा धनात्मक x-दिशा के अनुदिश है
B. तब बिन्दु P जिसके निर्देशांक `(0m, +(R )/(2)m)` है पर विद्युत विभव (वोल्ट में) शून्य होगा
C. तब वलय का द्विध्रुव आघूर्ण `(4R^(2)lambda) hati` C-m है।
D. तब वलय का द्विध्रुव आघूर्ण `(2R^(2)lambda) hati` C-m है।

Answer

A::B::C

Explanation

माना कि वलय के दो छोटे भाग जिन पर आवेश +dq और –dq है, y-अक्ष के परितः सममिति रूप से स्थित है। इस युग्म के कारण y-अक्ष पर किसी बिन्दु पर विभव शून्य होगा। ऐसे सभी संभव युग्मों के विभवों का योग y-अक्ष पर सभी बिन्दुओं पर शून्य होगा अतः `P(0, (R )/(2))` पर विभव शून्य है।

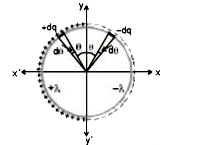
चूँकि सभी आवेश x-y तल में स्थित है, इसलिए बिन्दु P पर विद्युत क्षेत्र की दिशा x-y तल में होनी चाहिए। y-अक्ष समविभव (शून्यविभव) रेखा भी है। अतः y-अक्ष पर सभी बिन्दुओं पर विद्युत क्षेत्र की दिशा y-अक्ष के लम्बवत् होनी चाहिए। अतः P पर विद्युत क्षेत्र की दिशा x-y तल में होनी चाहिए और y-अक्ष के लम्बवत् होनी चाहिए। अतः विद्युत क्षेत्र की दिशा धनात्मक x-अक्ष के अनुदिश होगी।

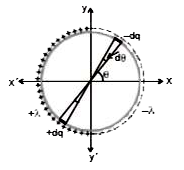
माना कि वलय के दो छोटे भाग जिन पर आवेश +dq और –dq है जैसा कि चित्र में दिखाया गया है। यह युग्म एक द्विध्रुव बनाता है, जिसका द्विध्रुव आघूर्ण है
`dp=dq 2R= (lambda Rd theta) 2R`
तंत्र का परिणामी द्विध्रुव आघूर्ण ऐसे सभी आवेशों के युग्मों के द्विध्रुव आघूर्णी का सदिश योग है। सममिति से,
परिणामी द्विध्रुव आघूर्ण ऋणात्मक x-अक्ष के अनुदिश है
`:.` नेट द्विध्रुव आघूर्ण `= - int_(-pi//2)^(+pi//2) (dp cos theta) hati= - int_(+pi//2)^(+pi//2) (2lambda R^(2) cos theta d theta) hati`
`= -4R6(2)lambda hati`