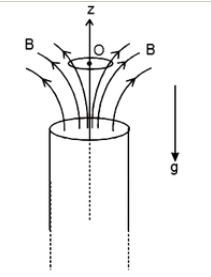
एक पतली अति चालक (शून्य प्रतिरोध) की एक वल्य ऊर्ध्वाधर लम्बी परिनालिका के ऊपर चित्रानुसार रखी हुई है | वल्य की सममित अक्ष परिनालिका की अक्ष के समान है | वलय के चारों ओर बेलनाकार सममित चुंबकीय क्षेत्र को चुंबकीय क्षेत्र सदिश के ऊर्ध्वाधर तथा त्रिज्यीय घटक के पदों में $B_{z} = B_{0} (1 - α z)$ तथा $B_{r} = B_{0} β r$ के अनुसार दर्शाया जा सकता है, जहाँ $B_{0}, α$ तथा $β$ धनात्मक नियतांक है तथा z व r क्रमश: ऊर्ध्वाधर तथा त्रिज्यीय स्थितियों के निर्देशांक हैं | प्रारम्भ में वलय का तल क्षैतिज है तथा इसमें कोई धारा प्रवाहित नहीं है | जब इसे छोड़ा जाता हैं तो यह इसकी ऊर्ध्वाधर अक्ष के अनुदिश नीचे की ओर गति प्रारम्भ करती है | वलय के केंद्र 'O' का प्रारम्भिक निर्देशांक z = 0 तथा r = 0 है |
दिए गए चित्र में बिंदु O अक्ष पर स्थित हैं तथा यह परिनालिका के थोड़ा सा ऊपर है | 'O' के ऊर्ध्वाधर तथा त्रिज्यीय स्थिति निर्देशांक (0, 0) है, वलय का द्रव्यमान m, त्रिज्या $r_{0}$ तथा स्वप्रेरकत्व L है | गुरुत्वीय मानें |

वलय के सरल आवर्त गति (z-अक्ष के अनुदिश अल्प विस्थापन के लिए) का आवर्तकाल ज्ञात कीजिए |

A

$\frac{1}{B_{0} r_{0}^{2}} \sqrt{\frac{2 m L}{α β}}$

B

$\frac{1}{2 B_{0} r_{0}^{2}} \sqrt{\frac{2 m L}{α β}}$

C

$\frac{1}{B_{0} r_{0}^{2}} \sqrt{\frac{m L}{3 α β}}$

D

इनमें से कोई नहीं

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

किसी स्थिति पर कुल चुंबकीय फ्लक्स $ϕ = B_{z} π r_{0}^{2} - L I$
चूँकि R = 0, अत: $ϕ = B_{0} (1 - α z) π r_{0}^{2} - L I$ = नियतांक
प्रारम्भिक शर्त से (z = 0, I = 0), नियतांक का मान $ϕ = B_{0} π r_{0}^{2}$
वलय में धारा की उपरोक्त समीकरण के उपयोग से $I = \frac{1}{L} B_{0} α π r_{0}^{2} z$
वलय पर कार्यरत लोरेंज बल (जो सममिती के कारण केवल ऊर्ध्वाधर हो सकता है) को निम्न प्रकार प्रदर्शित कर सकते हैं $F_{z} = - B_{r} I (z) 2 π r_{0} = - \frac{2 B_{0}^{2} α β π^{2} r_{0}^{4} z}{L} = - k z$
वलय की गति के समीकरण से $m a_{z} = f_{z} - m g = - k z - m g$
साम्यावस्था स्थिति $z_{0} = - m g / k$
$ω_{0} = \sqrt{\frac{k}{m}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

RESONANCE HINDI-PHYSICS( DPP NO -75)-BOARD PROBLEMS

Home
Ask Doubt
Profile