एक 20 ग्राम के कण पर निम्न दो सरल आवर्त गतियाँ अध्यारोपित है -
x1=2sin10t,
x2=4sin(10t+π3). जहाँ x1 व x2 मीटर में तथा t सेकण्ड में है
t=0 पर कण का विस्थापन 2√3 मी. होगा
कण की महत्तम चाल 20√7 मी./से. होगी
कण का महत्तम त्वरण का परिमाण 200√7 मी./से2 होगा
परिणामी गति की ऊर्जा 50 J होगी
The correct Answer is:A, B, C
t=0 पर
विस्थापन x=x1+x2=4sinπ3=2√3m.
परिणामी आयाम A=√22+42+2(2)(4)cosπ/3=√4+16+8=√28=2√7m
महत्तम चाल =Aω=20√7m/s
महत्तम त्वरण =Aω2=200√7m/s2
गति की ऊर्जा =12mω2A2=28J
Topper's Solved these Questions
Similar Questions
एक एकसमान प्रत्यास्थ छड़ जिसका काट क्षेत्र A है तथा प्राकृतिक लम्बाई L तथा यंग प्रत्यास्थता गुणांक Y है इसको एक चिकने क्षैतिज सतह पर रखा जाता है। अब दो क्षैतिज बल (जिनके परिणाम F व 3F है) को चढ़ के लम्बाई के अनुदिश चित्रानुसार एक दूसरे के विपरीत दिशा में सिरों पर चित्रानुसार लगाया जाता है। जब छड़ स्थायी अवस्था प्राप्त कर लेती है तो उस समय छड़ का विस्तार होगा -
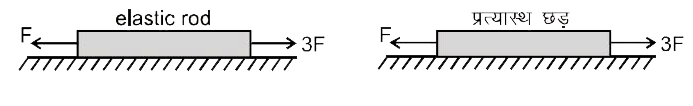
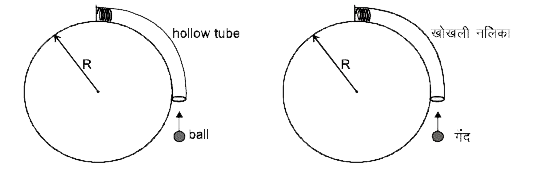
View Solutionचित्र में दर्शाए अनुसार द्रव्यमान M=2m तथा त्रिज्या R की क्षैतिज चकती पर द्रव्यमान m तथा काट क्षेत्र की अल्प त्रिज्या वाली खोखली नलिका व्यवस्थित की गई है। पूरे निकाय को चिकनी क्षैतिज मेज पर रखा गया है। एक हल्की स्प्रिंग (स्प्रिंग नियतांक k) नलिका के एक बंद सिरे पर जुडी है। नलिका के खुले सिरे में चाल v से द्रव्यमान m की एक छोटी गेंद रपर्श रेखीय प्रविष्ट होती है। चकती अपने केंद्र से पारित स्थिर उर्ध्व अक्ष के परितः घूर्णन करने के लिए स्वतंत्र है। आगे की गति में स्प्रिंग का अधिकतम संकुचन होगा:
View SolutionFor 0<x1<x2<π2, prove that x2x1<tanx2tanx1
View SolutionIf the mean of x_(1) and x_(2), and that of x_(1),x_(2),x_(3),x_(4) is M_(2), the mean of x_(1)+(x_(2))/(a),x_(3)+a,x_(4)-a is
View SolutionIf x_(1)+x_(2)=(pi)/(2) and x_(2)+x_(3)=x_(1), then tan x_(1)=tan x_(2)+lambda tan x_(3) where lambda is equal to
View SolutionIf x1x2x3=4(4+x1+x2+x3) then what is the value of [12+x1]+[12+x2]+[12+x3]?
View SolutionIf x_(1),x_(2),x_(3) are the roots of x^(3)+ax^(2)+b=0, the value of x_(2)x_(3),x_(1)x_(3),x_(1),x_(2)]|
View SolutionA 20gm particle is subjected to two simple harmonic motions
x1=2sin10t,
x2=4sin(10t+π3), where x1&x2 are in metre &t is in sec.
View Solution20, मापनो x1,x2,x3,...........x20 का औसत y, है। तब, (x1−101),(x2−101),(x3−101)......(x20−101) का औसत ज्ञात करे?
View Solutionसिद्ध कीजिए कि:
∣∣ ∣∣1+x1x2x3x11+x2x3x1x21+x3∣∣ ∣∣=1+x1+x2+x3.
View SolutionIf x_(1),x_(2),….x_(20) are in H.P then x_(1)x_(2)+x_(2)x_(3)+….+x_(19)x_(20) =
View Solutionx1+x2≤1,−3x1+x2≥3,(x1,x2≥0) द्वारा निरूपित सुसंगत क्षेत्र है
View SolutionFind the value of (x1+x3+x4−x2) for the equation (3+x1+x2+x3+x4)5=9375x1x2x3x4, where x1,x2,x3,x4>0
View SolutionIf x1,x2=3,x3+x4=12 and x1,x2,x3,x4 are in increasing G.P then the equation having x1,x2 as roots is
View SolutionFind all solution (x1,x2,x3,......xn) of the equation:
1+1x1+x1+1x1x2+.........+(x1+1)(x2+1)....(xn+1+1)x1x2......xn=0
View Solution
