dydx=cos(x+y)−sin(x+y) को हल कीजिए |
The correct Answer is:x + c
dydx=cos(x+y)−sin(x+y)
.....(i)
x+y=t रखने पर
1+dydx=dtdx
dydx=dtdx−1
अतः समी (i) से
dtdx−1=cost−sint
⇒dtdx=1+cost−sint
⇒∫dt1+cost−sint=∫dx
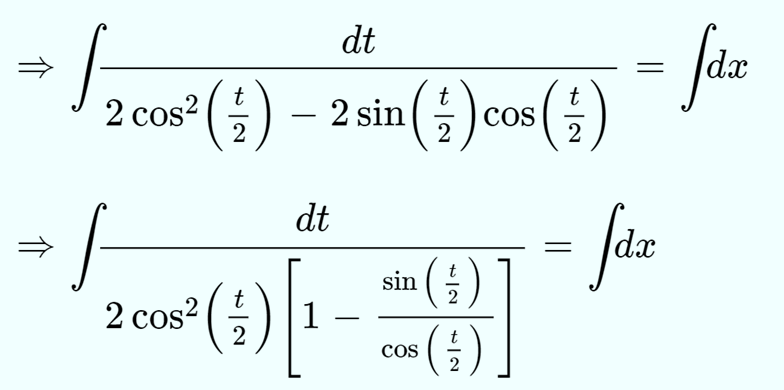
⇒∫sec2(t2)dt2[1−tan(t2)]=∫dx
⇒−log∣1−tanx+y2∣∣∣
=x+c
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONBOOK - ALLEN HINDICHAPTER - DIFFERENTIAL EQUATIONEXERCISE - Do yourself
39 Videos
- DIFFERENTIAL EQUATIONBOOK - ALLEN HINDICHAPTER - DIFFERENTIAL EQUATIONEXERCISE - EXERCISE - 01 (SELECT THE CORRECT ALTERNATIVE (ONLY ONE CORRECT ANSWER))
21 Videos
- DIFFERENTIABILITYBOOK - ALLEN HINDICHAPTER - DIFFERENTIABILITYEXERCISE - Exercise-5 [B]
15 Videos
- ELLIPSEBOOK - ALLEN HINDICHAPTER - ELLIPSEEXERCISE - EXERCISE - 05 - (B)
16 Videos
Similar Questions
निम्न अवकल समीकरणों की कोटि तथा घात ज्ञात कीजिए :
[1+(y')]1/2=x2+y
View Solutionअवकल समीकरण (1+3dydx)23=4d3ydx3 की कोटि व घात है.
View Solutionयदि f:R→R एक फलन जो f(x)=max(x,x3) द्वारा परिभाषित है तब उन बिंदुओं का समुच्चय जहां f(x), अवकलनीय नहीं है
View Solutionमाना C1 तथा C2 दो वृत्त हैं, C2,C1 के अन्दर स्थित है। एक वृत्त, C,C1 के अन्दर स्थित है तथा C1 को अन्तः तथा C2 को बाह्य स्पर्श करता है। C के केन्द्र का बिन्दुपथ ज्ञात कीजिए।
View Solutionहल कीजिए- dydx+ytanx=y2secx
View Solutionनिम्न अवकल समीकरण को हल कीजिए :
xsinyxdy=(ysinyx−x)dx.
View Solutionनिम्न अवकल समीकरण को हल कीजिए :
dydx=yx+√x2+y2x.
View Solutionहल कीजिए -
dydx−yx+tan(yx)
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए -
(sinx+cosx)dy+(cosx−sinx)dx=0
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
हल कीजिए -
dydx=1x+y+1
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
(x+y)(dx−dy)=dx+dy
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
x+y=sin−1(dydx)
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
dydx=(x−y)+32(x−y)+5
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए -
dydx=ex−y(ex−ey)
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए -
tanxcosydydx+siny−esinx=0
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए -
dydx+xsin2y=x3cos2y
View Solution
