Given with , Points x and y are taken on AB and AC respectively so thatAX = AY. If Area of area of find AX.
15
16
17
14
The correct Answer is:A
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE SHEET (EXERCISE-III) (LEVEL-I) (Straight Objective Type Questions)
42 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE SHEET (EXERCISE-III) (LEVEL-II) (Straight Objective Type Questions)
39 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE SHEET (EXERCISE-II) (LEVEL-I)
32 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
Knowledge Check
In ΔABC, D and E are two points on the sides AB and AC respectively so that DE || BC and ADBD=23. Then the area of trapezium DECBthe area of ΔABCequa to
A59B2125C145D514ΔABC is an equilateral triangle and D and E are midpoints of AB and BC respectively. Then the area of ΔABC : the area of the trapezium ADEC is
A5:3B4:1C8:5D4:3
In a triangle ABC, X and Y are points on the segments AB and AC, respectively, such that AX:XB=1:2 and AY:YC=2:1. If the area of triangle AXY is 10 then what is the area of triangle ABC?
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC

View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC

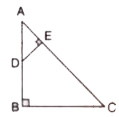
View SolutionIn ΔABC,∠B=90∘,AB=12cmandAC=15cm. D and E are points on AB and AC respectively such that ∠AED=90∘ and DE = 3 cm. Calculate the area of ΔABC and then the area of ΔADE.
View SolutionSuppose ABC is a triangle with AB of unit length. D and E are the points lying on AB and AC respectively such that BC and DE are parallel. If the area of triangle ABC is twice the area of triangle ADE, then the length of AD is
View SolutionIn a triangle ABC,XandY are the points on ABandBC respectively. If BX=12ABandBY=12BCandAB=BC. Show that BX=BY.
View Solution

