The curve is given by x=cos2t,y=sint represents
A
A parabola
B
Circle
C
Part of a parabola
D
A pair of straight lines
Video Solution
Text Solution
The correct Answer is:C
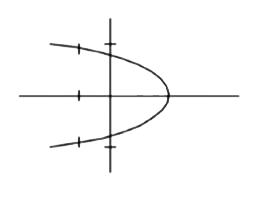
Given parabola equations are
x=cos2t,y=sint
⇒ Obviously, x,y∈[−1,1]
∴x=1−2sin2t=1−2y2
⇒2y2=1−x=−(x−1)
⇒y2=−12(x−1)
⇒ It represents a part of a parabola
|
Similar Questions
Knowledge Check
The curve is given by x=cos2t,y=sint represents
AA parabolaBCircleCPart of a parabolaDA pair of straight linesIf the parametric of a curve given by x=etcost,y=etsint, then the tangent to the curve at the point t=π/4 makes with axis of x the angle
A0Bπ/4Cπ/3Dπ/2The curve represented by x = 3 (cos t + sin t), y = 4 (cos t- sin t) is an ellipse whose eccentricity is e, such that 16e2+7 is equal to:
A14B12C11D21
x=sint,y=cos2t
View SolutionIf a curve is given by x=acost+b2cos2t and y=asint+b2sin2t, then the points for which d2ydx2=0, are given by
View SolutionThe curve represented by x=2(cost+sint)andy=5(cost−sint) is
View SolutionThe distance, from the origin, of the normal to the curve, x=2cost+2tsint,y=2sint−2tcos t at t=π4, is :
View SolutionIf OT is the perpendicular drawn from the origin to the tangent at any point t to the curve x=acos3t,y=asin3t, then OT is equal to :
View Solution
