The curve is given by $x = cos 2 t, y = sin t$ represents

A

A parabola

B

Circle

C

Part of a parabola

D

A pair of straight lines

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

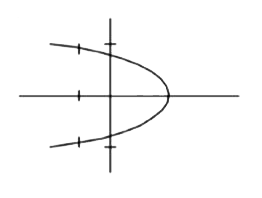
Given parabola equations are
$x = cos 2 t, y = sin t$
$\Rightarrow$ Obviously, $x, y \in [- 1, 1]$
$∴ x = 1 - 2 {sin}^{2} t = 1 - 2 y^{2}$
$\Rightarrow 2 y^{2} = 1 - x = - (x - 1)$
$\Rightarrow y^{2} = - \frac{1}{2} (x - 1)$
$\Rightarrow$ It represents a part of a parabola

|

Updated on:21/07/2023

Class 11 MATHS QUIZ

Similar Questions

Knowledge Check

Question 1 - Select One
The curve is given by $x = cos 2 t, y = sin t$ represents
AA parabola
BCircle
CPart of a parabola
DA pair of straight lines
Question 2 - Select One
If the parametric of a curve given by $x = e^{t} cos t, y = e t sin t$ , then the tangent to the curve at the point $t = π / 4$ makes with axis of x the angle
A0
B $π / 4$
C $π / 3$
D $π / 2$
Question 3 - Select One
The curve represented by x = 3 (cos t + sin t), y = 4 (cos t- sin t) is an ellipse whose eccentricity is e, such that $16 e^{2} + 7$ is equal to:
A14
B12
C11
D21

VIDYAMANDIR CLASSES (VMC MODULES)-QUIZ-MATHEMATICS

Home
Ask Doubt
Profile