α,β,γ तथा δ बढ़ते हुए परिमाण में न्यूनतम धनात्मक कोण है, जिनकी जय एक धनात्मक संख्या k के बराबर है तो , 4sinα2+3sinβ2+2sinγ2+sinδ2 का मान है-
2√)(1−k)
2√1+k
2√k
2k
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
AB के लंबवत ED है , AB = 20 इकाई तथा AC=12 इकाई है।
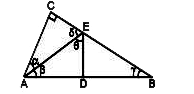
त्रिभुज AEC का क्षेत्रफल है-
View Solutionअंतराल [0,5π] में समीकरण 3sin2x−7sinx+2=0 के हेलो की संख्या होगी
View SolutionProve that: sinα+sinβ+sinγ−sin(α+β+γ)=4sin(α+β2)sin(β+γ2)sin(γ+α2).
View SolutionIf sinαsinβ=cosγcosδ,thensin(α−β2)⋅cos(α+β2)⋅cosδsin(δ−γ2)⋅sin(δ+γ2)⋅sinβ is equal to
View SolutionProve that : sinα+sinβ+sinγ−sin(α+β+γ)=4sin(α+β2).sin(β+γ2).sin(γ+α2)
View SolutionThe value of the determinant Δ=∣∣ ∣ ∣∣sin2αsin(α+β)sin(α+γ)sin(β+γ)sin2βsin(γ+β)(sinγ+α)sin(γ+β)sin2γ∣∣ ∣ ∣∣, is
A. 0
B. sin2α+sin2β+sin2γ
C. 32
D. None of these
View SolutionIf the angles α,β,γ of a triangle satisfy the relation,
sin(α−β2)+sin(α−γ2)+sin(3α2)=32, then
The measure of the smallest angle of the triangle is
View SolutionIf the angles α,β,γ of a triangle satisfy the relation,
sin(α−β2)+sin(α−γ2)+sin(3α2)=32, then
Triangle is
View SolutionIf α,β,γ are angles of a triangle then the value of (sin2α+sin2β+sin2γ−2cosαcosβcosγ) is-
View Solutionপ্রমাণ করো যে, sinα+sinβ+sinγ−sin(α+β+γ)=4sinα+β2sinβ+γ2sinγ+α2
View SolutionSupposeα,β,γ∈ R are such that sin α,sinβ,sinγ≠0
and Δ=∣∣ ∣ ∣∣sin2αsinαcosαcos2αsin2βsinβcosβcos2βsin2γsinγcosγcos2γ∣∣ ∣ ∣∣ then Δ cannot exceed
View SolutionIf the angles α,β,γ of a triangle satisfy the relation,
sin(α−β2)+sin(α−γ2)+sin(3α2)=32, then
The measure of the smallest angle of the triangle is
View SolutionIf the angles α,β,γ of a triangle satisfy the relation,
sin(α−β2)+sin(α−γ2)+sin(3α2)=32, then
Triangle is
View Solutionयदि α,β,γ त्रिभुज के कोण है तब sin2α+sin2β+sin2γ−2cosαcosβcosγ का मान है।
View SolutionA line makes angles α,β,γandδ with the diagonals of a cube, prove that sin2α+sin2β+sin2γ+sin2δ=83.
View SolutionIf the angles α,β,γ of a triangle satisfy the relation,sin(α−β2)+sin(α−γ2)+sin(3α2)=32, then
The measure of the smallest angle of the triangle is
View Solution
