ABCD is a square of side 2m. Charges of $5 n C, + 10 n C$ and $- 5 n C$ are placed at corners A,B and C respectively .What is the workdone in transferring a charge of 5nC from 'D' to the point of intersection of the diagonals ? Solution in Kannada

Video Solution

Text Solution

Verified by Experts

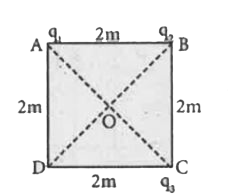
In the Fig. .O. represents the point of intersection of the diagonals.
AO=BO=CO=DO= $\sqrt{2}$
Total electric potential at .O. is
$V_{0} = \frac{1}{4 π ε_{0}} [\frac{q_{1}}{A O} + \frac{q_{2}}{B O} + \frac{q_{3}}{C O}]$
$= 9 \times 10^{9} [\frac{5 \times 10^{- 9}}{\sqrt{2}} + \frac{10 \times 10^{- 9}}{\sqrt{2}} - \frac{5 \times 10^{- 9}}{\sqrt{2}}]$
$= 9 \times 10^{9} \times 10^{- 9} [\frac{5}{\sqrt{2}} + \frac{10}{\sqrt{2}} - \frac{5}{\sqrt{2}}]$
=9[3.536+7.072-3.536]
$V_{0}$ =63.648 volt
Total electric potential at D is
$V_{D} = \frac{1}{4 π \in_{0}} [\frac{q_{1}}{A D} + \frac{q_{2}}{B D} + \frac{q_{3}}{C D}]$
$= 9 \times 10^{9} [\frac{5 \times 10^{- 9}}{2} + \frac{10 \times 10^{- 9}}{2 \sqrt{2}} - \frac{5 \times 10^{- 9}}{2}]$
$= 9 \times 10^{9} \times 10^{- 9} [\frac{5}{2} + \frac{5}{\sqrt{2}} - \frac{5}{2}]$
=9[25+3.536-2.5] = 31.824 volt
$∴$ Potential difference between O and D is
$V = V_{0} - V_{D}$ =63.648-31.824=31.824 volt
$∴$ Work required to transfer a charge of $5 \times 10^{- 9}$ C from D to O is
$w = V q = 31.824 \times 5 \times 10^{- 9}$
$w = 159.12 \times 10^{- 9}$ Joule .

|

Updated on:21/07/2023

Class 12 PHYSICS SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015

Topper's Solved these Questions

Similar Questions

SUNSTAR PUBLICATION-SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015-PART-D

Home
Ask Doubt
Profile