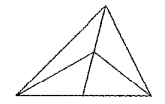
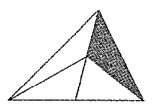
In the picture below, the top vertex of a triangle is joined to the midpoint of the bottom side of the triangle and then the midpoint of this line is joined to the other two vertices.
Prove that the areas of all four triangles obtained thus are equal to a fourth of the area of the whole triangle.
 Solution in Malayalam
Solution in Malayalam
Step by step video & image solution for In the picture below, the top vertex of a triangle is joined to the midpoint of the bottom side of the triangle and then the midpoint of this line is joined to the other two vertices. Prove that the areas of all four triangles obtained thus are equal to a fourth of the area of the whole triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
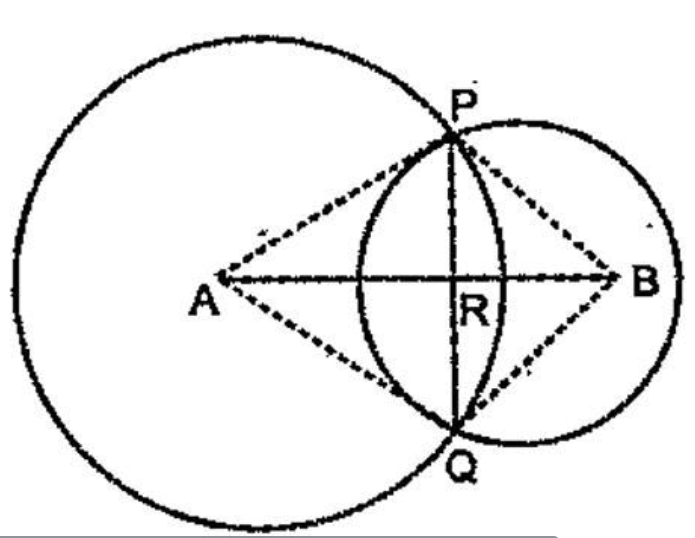
Prove that the line joining the centres of two intersecting circles is the perpendicular bisector of the line joining the points of intersection.
 01:37View Solution
01:37View SolutionHow many lines of symmetry does the above figure have ?
02:11View SolutionDetermine the point of symmetry of a regular hexagon.
01:31View SolutionDtermine the images of the following figure about the given line :
02:45View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionMatch the following Column A to Column B
 05:41View Solution
05:41View SolutionMatch the following Column A to Column B
 03:28View Solution
03:28View SolutionFind the area of figure given below.
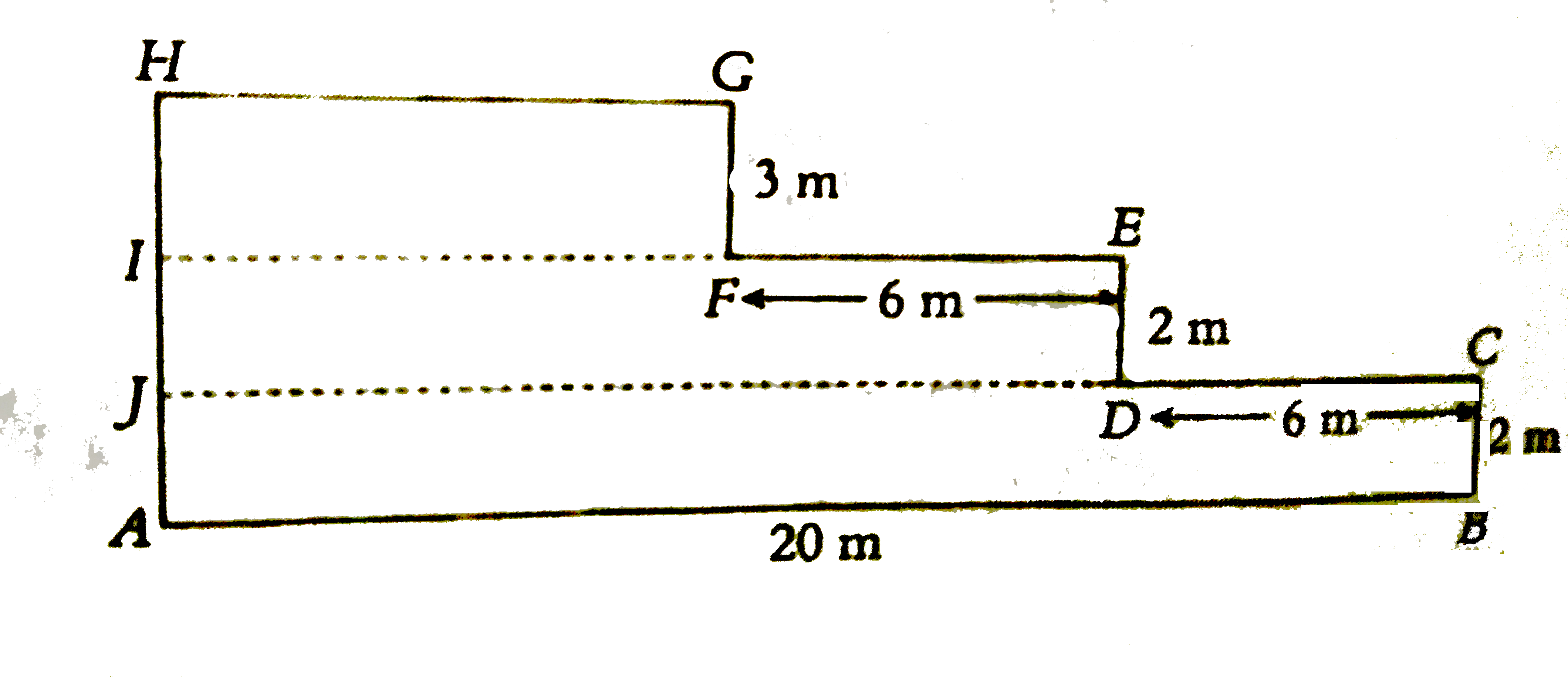 02:21View Solution
02:21View SolutionFind the area of the figure given below.
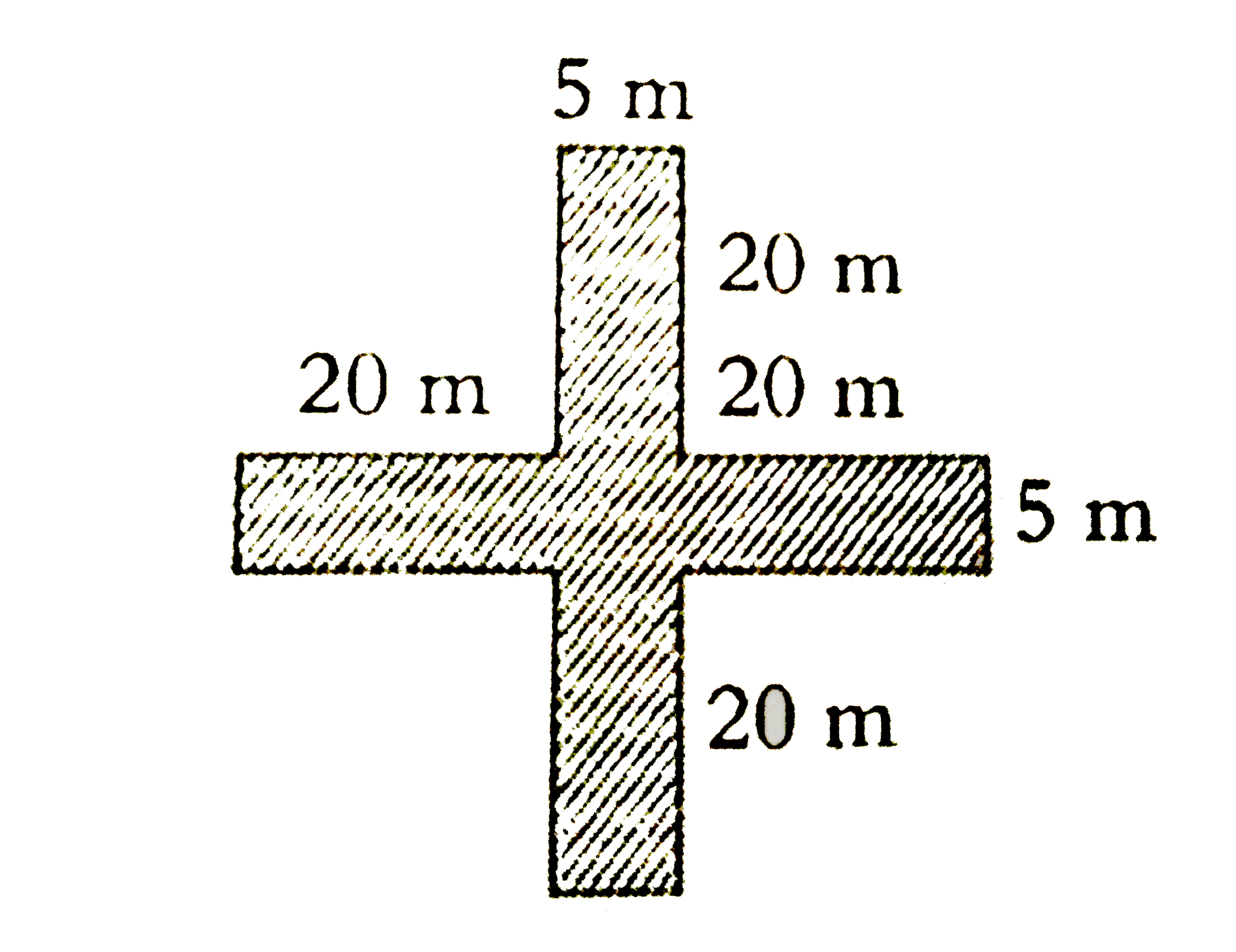 02:03View Solution
02:03View SolutionThe area of the shaded part in the figure given below is ______.
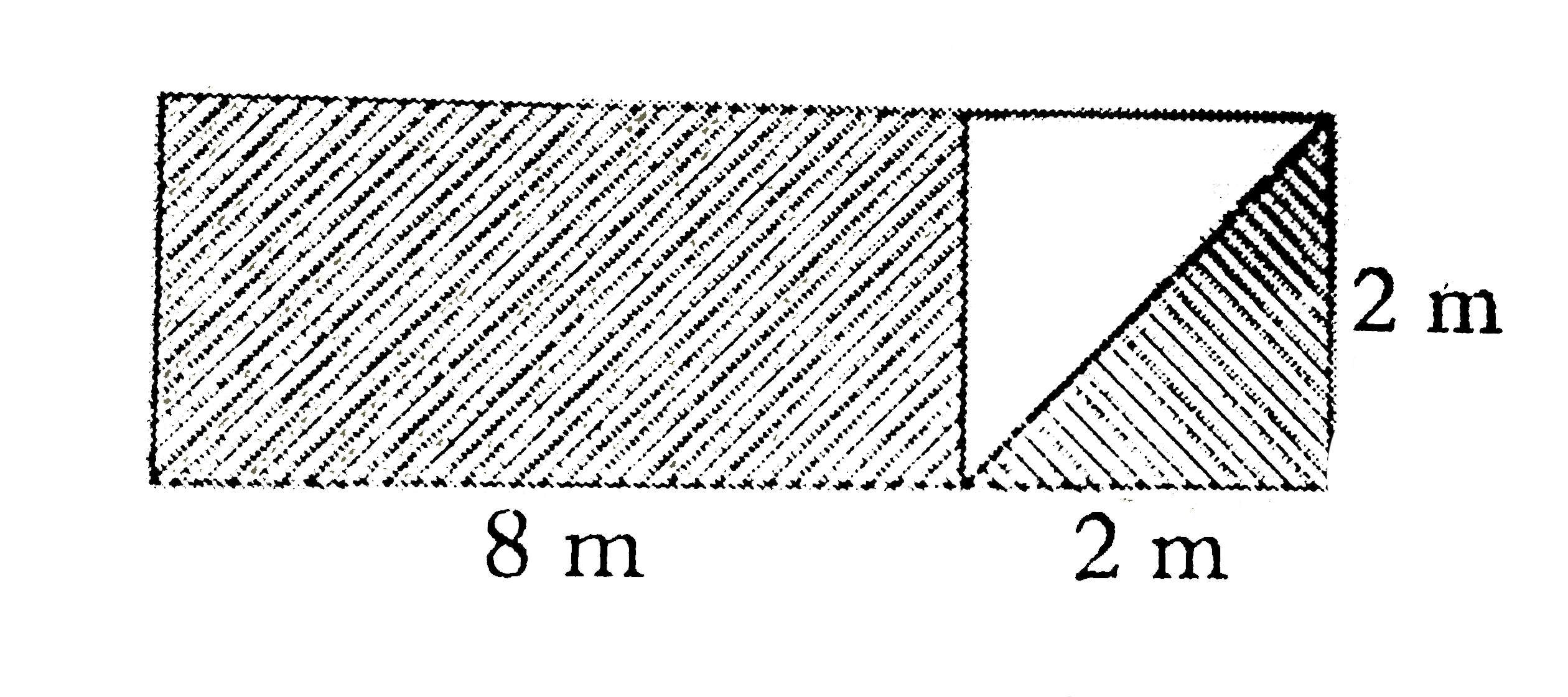 02:10View Solution
02:10View SolutionThe inequation represented by the graph given below is :
02:17View SolutionThe inequation that best describes the graph given below is _________
02:10View SolutionThe inequation that best describes the following graph is _________
01:57View SolutionFind out area of triangle OAB and BCD shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
01:52View SolutionThe total surface area of the given solid figure is _______________.
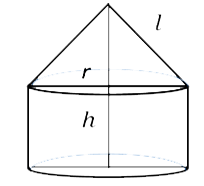 04:42View Solution
04:42View Solution

