Draw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that perpendicular bisects the bottom side of the larger triangle.
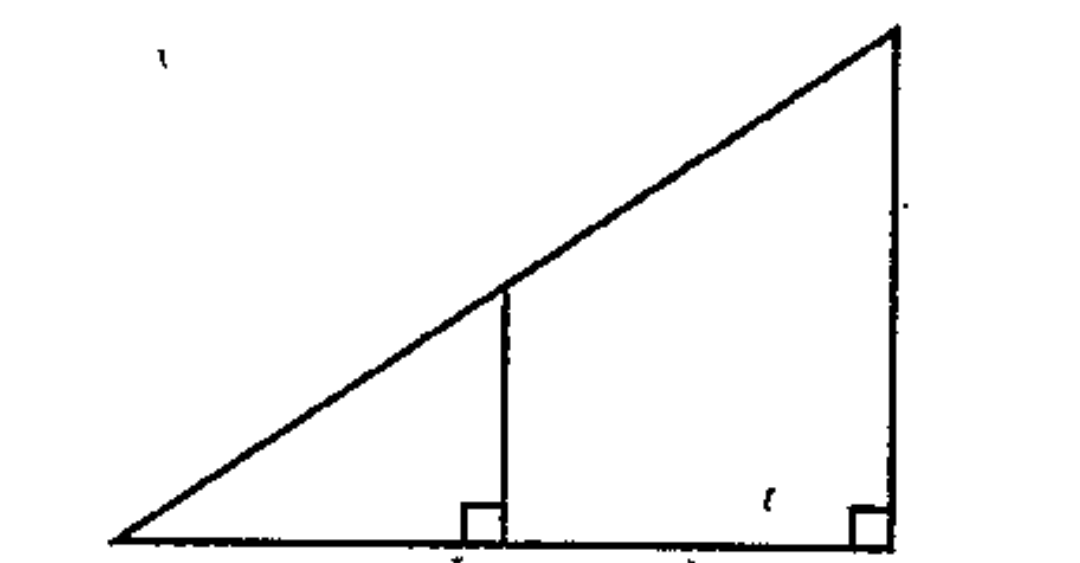.Solution in Malayalam
Step by step video & image solution for Draw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base Prove that perpendicular bisects the bottom side of the larger triangle. . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a rectangle of perimeter one metre, one side is five centimetres longer than the other. What are the length of the sides.
View SolutionThe perpendicular from the square corners of a right angle triangle cuts the opposite side into two parts of 2 and 3 cm length.Prove that two small triangles cut by the perpendicular have the same angles.
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionDraw the bisector of ∠AOB=58∘
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VII_C05_S01_009_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B
View SolutionMatch the following Column A to Column B
View SolutionMatch the following Column A to Column B
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionFind out area of triangle OAB and BCD shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
View SolutionDraw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that this perpendicular is half the perpendicular side of the large triangle.
.
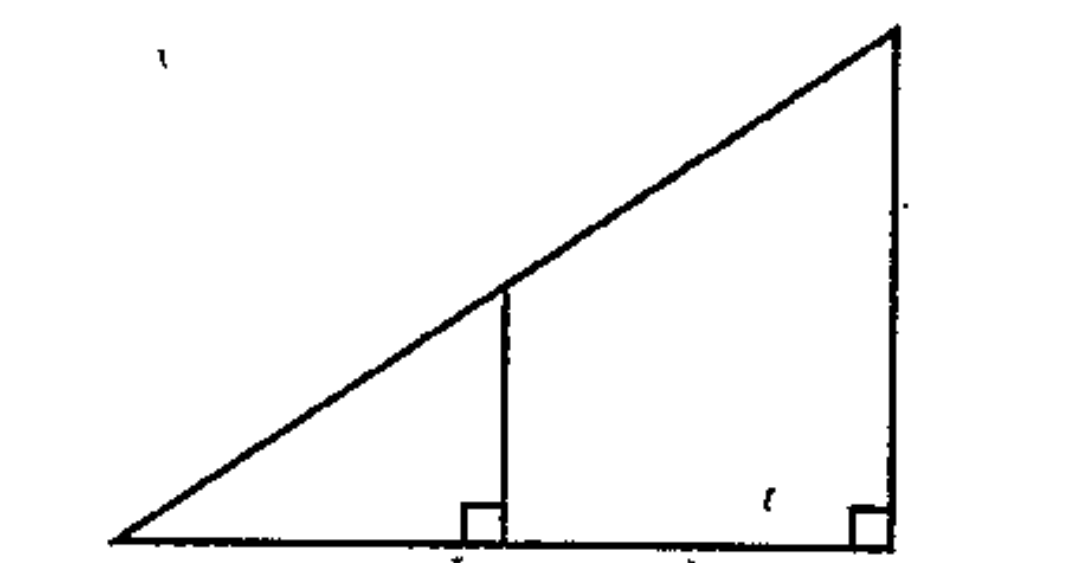View Solution