Consider the number 2751. The sum of its digital is . Adding the digits of 15 we get . This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe is . Sum of digits of . Sum of digits of . Therefore the digital root of is .
Digital roots have an interesting property. To see this, consider the product . The digital roots of the numbers and are and . Product of the digital roots=. Digital root of . The Digital root of 1161 is also that is the digital root of , where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
What is the digital root of 927?Solution in Malayalam
Step by step video & image solution for Consider the number 2751. The sum of its digital is 2+7+5+1=15. Adding the digits of 15 we get 1+5=6. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit) Let us see one more example. The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29. Sum of digits of 29=2+9=11. Sum of digits of 11=1+1=2. Therefore the digital root of 679412 is 2. Digital roots have an interesting property. To see this, consider the product 43times27=1161. The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9. Product of the digital roots=7times9=63. Digital root of 63=6+3=9. The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=The digital root of 63, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers. What is the digital root of 927? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
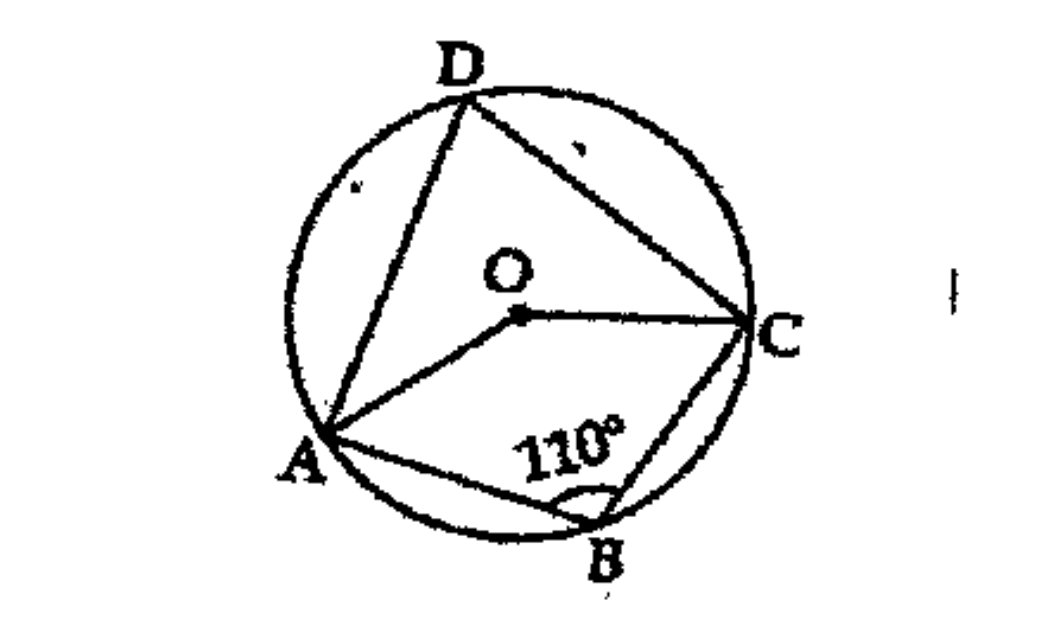
In the figure, O is the centre of the circle and A,B,C,D are points on it.
If ∠B=110o, then
What is the measure of ∠D?
 .03:40View Solution
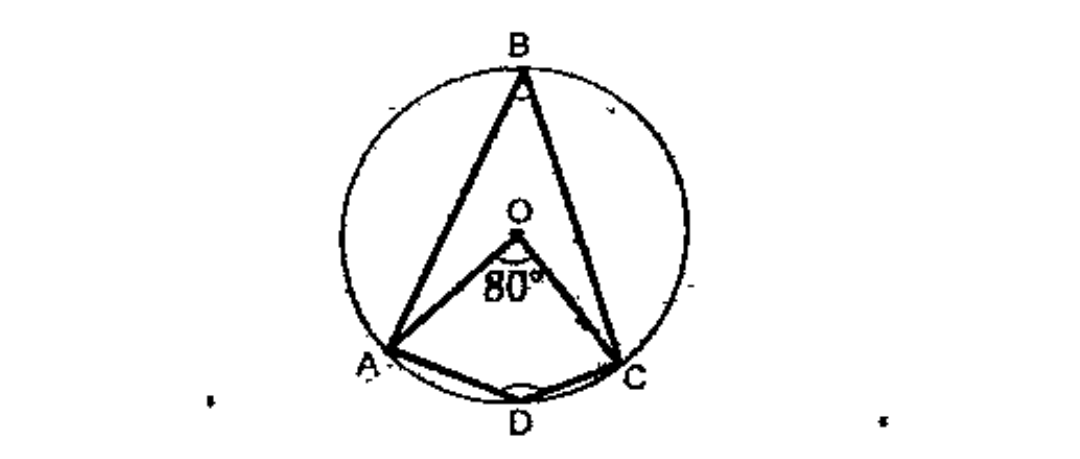
.03:40View SolutionIn the figure O is the centre of circle. □AOC=80o
What is the measure of □ABC?
 .03:24View Solution
.03:24View Solutionदों अंकों की एक संख्या अपने अंकों के योग के तीन गुनी है । यदि उस संख्या में 45 जोड़ दिया जाता है तो उसके अंकों का स्थान बदल जाता है तो उस संख्या के अंकों का योग ज्ञात करें।
02:36View Solutionदों अंकों की एक संख्या में दहाई स्थान का अंक इकाई स्थान के अंक से 5 अधिक है। यदि अंकों के योग का पांच गुना उस संख्या में से घटाया जाता है तो उस संख्या के अंकों का स्थान बदल जाता है तो संख्या के अंकों का योग ज्ञात करें।
04:23View SolutionThe unit digit of a two digit number is 6. If 9 is added to the number ,then 5/4th of the number itself. Find the sum of the digits
00:59View SolutionIn a two-digit number, the sum of the digit is 5 more than the units digit. The difference between the original number and the sum of digits is 10 more than the number formed by reversing the digits. Then find the difference between the digits.
02:28View SolutionThe digit of a 2-digit number in a unit is 5 and the sum of the digits is the (1/5) of the original number Find the number.
05:52View Solutionएक दो अंकों की संख्या तथा उसके अंकों को उलटने पर बनी संख्या का योग 132 है। यदि इस संख्या में 12 जोड़ा जाये तो नै, संख्या, अंकों के योग से 5 गुनी होगी। संख्या ज्ञात कीजिए।
02:59View SolutionA three digit number is equal to 17 times the sum of its digits. If 198 is added to the number, the digits get reserved. The sum of the extreme digits is 1 less than the midle digit. Find the number.
03:02View SolutionThe sum of the digits of a 2-digits number is 6. The number obtained by interchangind its digits is 18 more than the original number. Find the original number.
04:32View Solutionएक संख्या दो अंकों की है । दहाई का अंक इकाई के अंक से 6 बड़ा है । यदि यह संख्या अंकों के योग का 10 गुना है । तो संख्या ज्ञात करें ।
01:30View Solutionएक संख्या दो अंकों की है । दहाई का अंक इकाई के अंक से 4 बड़ा है । यदि अंकों का योग संख्या का 17 गुना है, तो संख्या ज्ञात करें ।
04:54View SolutionConsider the number 2751. The sum of its digital is 2+7+5+1=15. Adding the digits of 15 we get 1+5=6. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29. Sum of digits of 29=2+9=11. Sum of digits of 11=1+1=2. Therefore the digital root of 679412 is 2.
Digital roots have an interesting property. To see this, consider the product 43×27=1161. The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9. Product of the digital roots=7×9=63. Digital root of 63=6+3=9. The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=Thedigitalo√f63, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
What is the digital root of 345?05:23View SolutionConsider the number 2751. The sum of its digital is 2+7+5+1=15. Adding the digits of 15 we get 1+5=6. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29. Sum of digits of 29=2+9=11. Sum of digits of 11=1+1=2. Therefore the digital root of 679412 is 2.
Digital roots have an interesting property. To see this, consider the product 43×27=1161. The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9. Product of the digital roots=7×9=63. Digital root of 63=6+3=9. The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=The digital root of 63, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
What is the digital root of 345×927?05:20View SolutionConsider the number 2751. The sum of its digital is 2+7+5+1=15. Adding the digits of 15 we get 1+5=6. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29. Sum of digits of 29=2+9=11. Sum of digits of 11=1+1=2. Therefore the digital root of 679412 is 2.
Digital roots have an interesting property. To see this, consider the product 43×27=1161. The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9. Product of the digital roots=7×9=63. Digital root of 63=6+3=9. The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=Thedigitalo√f63, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
The digital root of the number 63□5 is 8 (square represents a missing digit). Find the missing digit.05:53View Solution

