10 से 12 नीचे दिए गए गद्यांश को ध्यानपूर्वक पढ़िए एवं पूछे गए प्रश्नो के उत्तर दीजिए :
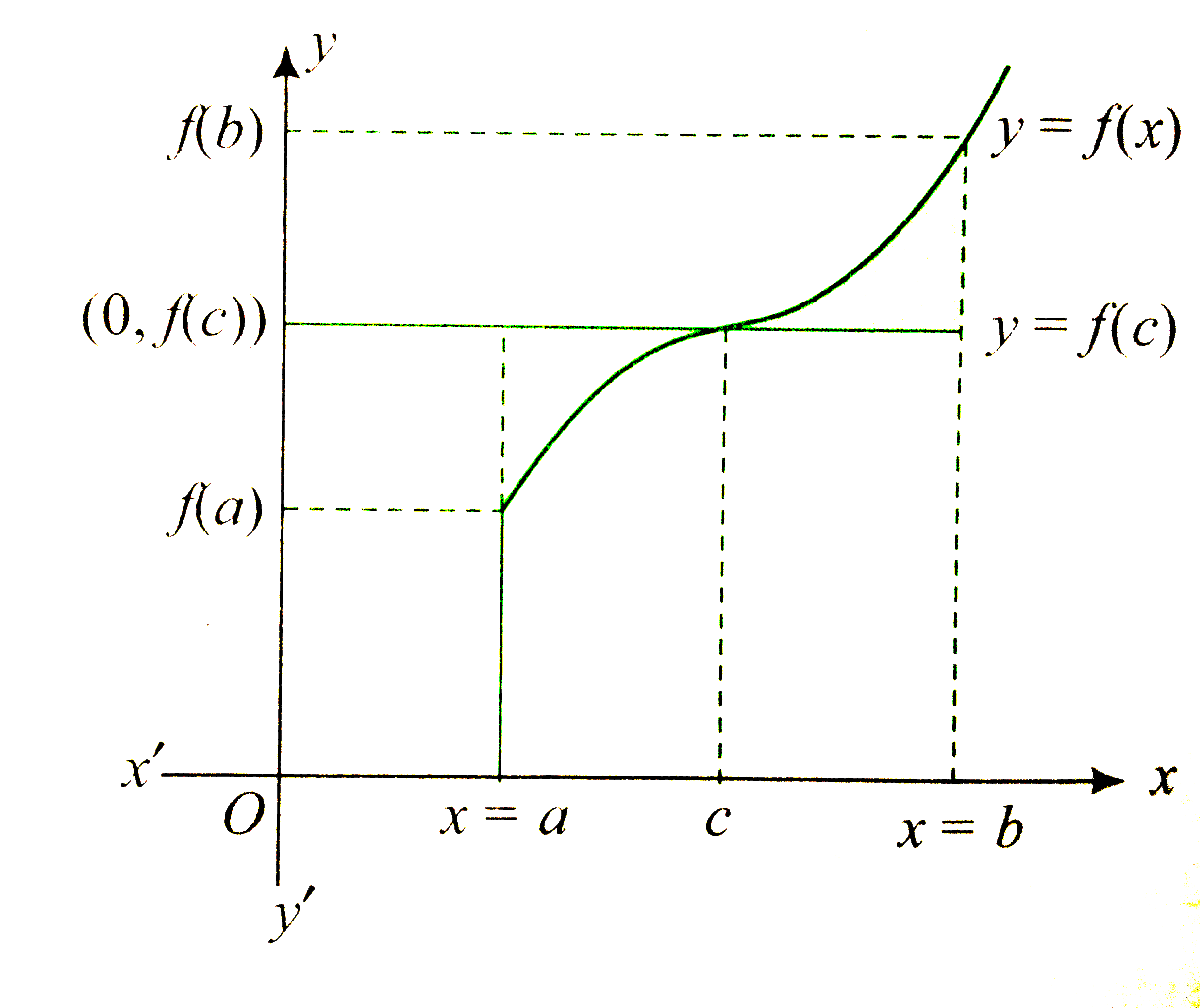
यदि निश्चित समाकल निम्न सूत्र के द्वारा परिभाषित हो, ∫baf(x)dx=b−a2(f(a)+f(b)), तथा c∈(a,b) के लिए अधिक यथार्थ मान ज्ञात करने के लिए F(c)=c−a2(f(a)+f(c))+b−c2(f(b)+f(c)) का प्रयोग कीजिए तथा जब c=a+b2 तो ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c))
प्रत्येक x∈(a,b) के लिए f'(x)<0 तथा बिन्दु c इस प्रकार है कि a<c<b तथा (c,f(c)) वक्र पर स्थित वह बिन्दु है जिसके लिए F(c) उच्चतम हो तो f'(c) का मान होगा -
f(b)−f(a)b−a
2(f(b)−f(a))b−a
2(f(b)−f(a))2b−a
0
The correct Answer is:A
Step by step video, text & image solution for 10 से 12 नीचे दिए गए गद्यांश को ध्यानपूर्वक पढ़िए एवं पूछे गए प्रश्नो के उत्तर दीजिए : यदि निश्चित समाकल निम्न सूत्र के द्वारा परिभाषित हो, int_(a)^(b)f(x)dx=(b-a)/(2)(f(a)+f(b)), तथा c in (a,b) के लिए अधिक यथार्थ मान ज्ञात करने के लिए F(c )=(c-a)/(2)(f(a)+f(c ))+(b-c)/(2)(f(b)+f(c )) का प्रयोग कीजिए तथा जब c=(a+b)/(2) तो int_(a)^(b)f(x)dx=(b-a)/(4)(f(a)+f(b)+2f(c)) प्रत्येक x in (a,b) के लिए f'(x)lt0 तथा बिन्दु c इस प्रकार है कि altcltb तथा (c,f(c)) वक्र पर स्थित वह बिन्दु है जिसके लिए F(c) उच्चतम हो तो f'(c) का मान होगा - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 05 A34videos
DEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -05 [B] (JEE-ADVANCED: PREVIOUS YEAR QUESTIONS)2videos
CONTINUITY
- BOOK - ALLEN HINDICHAPTER - DETERMINANTEXERCISE - DO YOURSELF -91videos
DETERMINANT
Similar Questions
यदि In=∫π/40tannxdx तब n(In−1+In+1) का मान है -
05:41View Solutionफलन f(x)=⎧⎨⎩e1/x−1e1/x+1जबx≠01जबx=0 का x=0 पर सततता का परीक्षण कीजिए।
02:55View Solutionसमीकरण निकाय λx+y+z=0,−x+λy+z=0,−x−y+λz=0 का एक अशून्य हल होगा यदि λ का वास्तविक मान है
01:45View SolutionWhich of the following is incorrect? ∫b+ca+cf(x)dx=∫baf(x+c)dx ∫bcacf(x)dx=c∫baf(cx)dx ∫a−af(x)dx=12∫a−a(f(x)+f(−x)dx None of these
01:40View SolutionSuppose we define the definite integral using the following formula ∫baf(x)dx=b−c2(f(a)+f(b)) , for more accurate result for c∈(a,b)F(c)=b−c2(f(a)−f(c))+b−c2(f(b)−f(c)). When c=a+b2,∫baf(x)dx=b−a4(f(a)+f(b)+f(2f(c)) then ∫π20sinxdx
05:39View SolutionLet the definite integral be defined by the formula ∫baf(x)dx=b−a2(f(a)+f(b)). For more accurate result, for cε(a,b), we can use ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx=F(c) so that for c=a+b2 we get ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
If f''(x)<0∀xε(a,b) and c is a point such that a<c<b, and (c,f(c)) is the point lying on the curve for which F(c) is maximum then f'(c) is equal toView SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is02:33View SolutionFor every function f (x) which is twice differentiable , these will be good approximation of
∫baf(x)dx=(b−a2){f(a)+f(b)}, for more acutare results for c∈(a,b),F(c)=c−a2[f(a)−f(c)]+b−c2[f(b)−f(c)]
When c=a+b2
∫baf(x)dx=b−a4{f(a)+f(b)+2f(c)}dx
If limt→a∫taf(x)dx−(t−a)2{f(t)+f(a)}(t−a)3=0, then degree of polynomial function f (x) atmost is04:02View SolutionFor every function f (x) which is twice differentiable , these will be good approximation of
∫baf(x)dx=(b−a2){f(a)+f(b)}, for more acutare results for c∈(a,b),F(c)=c−a2[f(a)−f(c)]+b−c2[f(b)−f(c)]
When c=a+b2
∫baf(x)dx=b−a4{f(a)+f(b)+2f(c)}dx
If f''(x)<0,∀x∈(a,b),and(c,f(c)) is point of maxima , where c∈(a,b), then f ' ( c) isView SolutionFor every function f (x) which is twice differentiable , these will be good approximation of
∫baf(x)dx=(b−a2){f(a)+f(b)}, for more acutare results for c∈(a,b),F(c)=c−a2[f(a)−f(c)]+b−c2[f(b)−f(c)]
When c=a+b2
∫baf(x)dx=b−a4{f(a)+f(b)+2f(c)}dx
Good approximation of ∫π/20sinxdx,is06:03View Solutionनिम्न अनुच्छेद को पढ़कर प्रश्नो के उत्तर दीजिए
एक द्विआवकलनीय फलन f(x) के लिए, ∫baf(x)≅(b−a2){f(a)+f(b)} एक अच्छा सन्निकट (approximation) है। यदि हम c=a+b2 ले, तब उपरोक्त को पुनः प्रयोग करने पर,
∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx≅b−a4{f(a)+f(b)+2f(c)}
∫π/20sinxdx का सन्निकट मान है03:37View Solutionनिम्न अनुच्छेद को पढ़कर प्रश्नो के उत्तर दीजिए
एक द्विआवकलनीय फलन f(x) के लिए, ∫baf(x)≅(b−a2){f(a)+f(b)} एक अच्छा सन्निकटन (approximation) है। यदि हम c=a+b2 ले, तब उपरोक्त को पुनः प्रयोग करने पर,
∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx≅b−a4{f(a)+f(b)+2f(c)}
यदि f''(x)<0,∀x∈(a,b) और [c,f(c)} एक उच्चिष्ठ बिन्दु है, जहाँ c∈(a,b) तो f'(c) है।04:35View SolutionLet the definite integral be defined by the formula ∫baf(x)dx=b−a2(f(a)+f(b)). For more accurate result, for cε(a,b), we can use ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx=F(c) so that for c=a+b2 we get ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
If f''(x)<0∀xε(a,b) and c is a point such that a<c<b, and (c,f(c)) is the point lying on the curve for which F(c) is maximum then f'(c) is equal to03:54View SolutionLet us define the definite integral with the following formula int_(a)^(b)f(x)dx = (b-a)/2 [f(a) +f(b)] c in (a,b) For more results above, F (c) = (c-a)/2 [f(a) +f(c) ] +(b-c)/2[f(b)+f(c)] when c=(a+b)/2, int _(a)^(b) f(x)d(x) = (b-a) /(4) [f(a) + f(b) + 2f(c)] int_(0)^(pi//2)sinx dx =
05:43View SolutionLet us define the definite integral with the following formula int_(a)^(b)f(x)dx = (b-a)/2 [f(a) +f(b)] c in (a,b) For more results above, F (c) = (c-a)/2 [f(a) +f(c) ] +(b-c)/2[f(b)+f(c)] when c=(a+b)/2, int _(a)^(b) f(x)d(x) = (b-a) /(4) [f(a) + f(b) + 2f(c)] If f''(x)lt 0 AAx in (a,b) And c is such a point that a lt c lt b And (c, f, (c)) is the point on the curve for which F (c) is the superlative, then f '(c) is equal to
03:21View SolutionProve that ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx, a<c<b
02:58View Solution

