Consider the points A(1,2,-1),B(2,5,1)andC(0,-1,-3):
Find −−→AB×−−→AC. Hence, prove that A,B,C are collinearSolution in Malayalam
Step by step video & image solution for Consider the points A(1,2,-1),B(2,5,1)andC(0,-1,-3):Find oversetrarr(AB)xxoversetrarr(AC). Hence, prove that A,B,C are collinear by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider the points A(0,0,2) and B(3,0,1) . Write direction ratio of the joining A and B.
View SolutionFind the value of 'a' for which the following points A(a,3),B(2,1) and C(5, a) are collinear. Hence find the equation of the line AC.
View SolutionIf the points A(−1,−4),B(b,c)andC(5,−1) are collinear and 2b+c=4, find the values of b and c
View SolutionFind the value of λ or which the points A(2,5,1) ,B(1,2,-1) and C(3,λ,3) are collinear .
View SolutionProve that the points A(a, 0), B(0, b) and C(1, 1) are collinear, if 1a+1b=1.
View SolutionIF the points (a,1),(1,2) and (0,b+1) are collinear. Then 1a+1b=…….
View SolutionShow that the points A(1,-2,-8),B(5,0,-2)andC(11,3,7) are collinear , and find the ratio in which B divides AC.
View SolutionShow that the points A(1,-2,-8),B(5,0,-2)andC(11,3,7) are collinear , and find the ratio in which B divides AC.
View SolutionShow that the points A(1,-2,-8),B(5,0,-2)andC(11,3,7) are collinear , and find the ratio in which B divides AC.
View SolutionConsider
A=[1x1],B=⎡⎢⎣1322511532⎤⎥⎦,C=⎡⎢⎣12x⎤⎥⎦
Find x if ABC=0.
View SolutionIf A=[12−21],B=[233−4]andC=[10−10] verify
(i) (A⋅B)⋅C=A⋅(BC)
(ii) A⋅(B+C)=AB+AC
View SolutionConsider the points A (5,1) ,B (1,-1) and C (11,4) Raju proved A,B,C are collinear by finding the equation of AB. write the steps written by Raju.
View SolutionConsider the points A (3,2,-4), B (5,4,-6) and C (9,8,-10).Find AB, BC and AC. Hence prove that A,B,C are collinear. Also find the ratio in which B divides AC.
View SolutionIn triangle ABC, which of the following is not true.
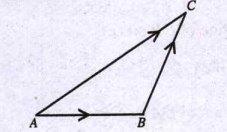a)−−→AB+−−→BC+−−→CA=→0
b)−−→AB+−−→BC−−−→AC=→0
c) −−→AB+−−→BC−−−→CA=→0
d)−−→AB−−−→CB+−−→CA=→0
View SolutionGiven that A,B,C are the points(2,1,−1),(3,2,−1)and(3,1,0).Find −−→AB and −−→AC.Hence, find the angle between−−→AB and −−→AC.
View Solution