There are three categories of jobs A,B and c . The average salary of the students who got the job of A and B categories is 26 lakh per annum. The average salary of the students who got the job of B and C category is 44 lakh per annum and the average salary of those students who got the job of A and C categories 34 lakh per annum. The most appropriate (or closest) range of average salary of all the three categories (if it is known that each student gets only one category of jobs i.e, A, B and C):
Lies between 30 and 40
lies between 28 and 34
lies between 34 and 43
lies between 29 and 48
The correct Answer is:A
To solve the problem, we need to find the average salary of three job categories A, B, and C based on the given average salaries of pairs of categories.
Let's denote:
- The average salary of category A as A
- The average salary of category B as B
- The average salary of category C as C
We have the following information from the question:
1. The average salary of students who got jobs in categories A and B is 26 lakh per annum:
A+B2=26⟹A+B=52(Equation 1)
2. The average salary of students who got jobs in categories B and C is 44 lakh per annum:
B+C2=44⟹B+C=88(Equation 2)
3. The average salary of students who got jobs in categories A and C is 34 lakh per annum:
A+C2=34⟹A+C=68(Equation 3)
Now, we have a system of three equations:
1. A+B=52
2. B+C=88
3. A+C=68
Step 1: Solve the equations
We can solve these equations step by step.
From Equation 1, we can express B in terms of A:
B=52−A(Equation 4)
Substituting Equation 4 into Equation 2:
(52−A)+C=88
C=88−52+A=36+A(Equation 5)
Now, substitute Equation 5 into Equation 3:
A+(36+A)=68
2A+36=68
2A=68−36
2A=32⟹A=16
Step 2: Find B and C
Now that we have A, we can find B and C using Equations 4 and 5.
Substituting A=16 into Equation 4:
B=52−16=36
Substituting A=16 into Equation 5:
C=36+16=52
Step 3: Calculate the average salary of all three categories
Now we have:
- A=16 lakh
- B=36 lakh
- C=52 lakh
To find the average salary of all three categories:
Average=A+B+C3=16+36+523=1043≈34.67 lakh
Conclusion
The average salary of all three categories is approximately 34.67 lakh per annum.
- The average salary of category A as A
- The average salary of category B as B
- The average salary of category C as C
A+B2=26⟹A+B=52(Equation 1)
B+C2=44⟹B+C=88(Equation 2)
A+C2=34⟹A+C=68(Equation 3)
1. A+B=52
2. B+C=88
3. A+C=68
B=52−A(Equation 4)
(52−A)+C=88
C=88−52+A=36+A(Equation 5)
A+(36+A)=68
2A+36=68
2A=68−36
2A=32⟹A=16
B=52−16=36
C=36+16=52
- A=16 lakh
- B=36 lakh
- C=52 lakh
Average=A+B+C3=16+36+523=1043≈34.67 lakh
Topper's Solved these Questions
Similar Questions
There are three categories of jobs A, B and C. The average salary of the students who got the job of A and B categories is 26 lakh per annum. The average salary of the students whogot the job of B and C category is 44 lakh per annum and the average salary of those students who got the job of A and C categories is 34 lakh per annum. The most appropriate (or closest) range of average salary of all the three categories (if it is known that each student gets only one category of jobs i. e.,A, B and C):
View SolutionThe average salary of A, B is Rs. 6000 and that of C, D and E is Rs. 8000. The average salary of all the 5 people is :
View Solution
Knowledge Check
- Question 1 - Select One
There are three categories of jobs A,B and c . The average salary of the students who got the job of A and B categories is 26 lakh per annum. The average salary of the students who got the job of B and C category is 44 lakh per annum and the average salary of those students who got the job of A and C categories 34 lakh per annum. The most appropriate (or closest) range of average salary of all the three categories (if it is known that each student gets only one category of jobs i.e, A, B and C):
Alies between 30 and 44Blies between 28 and 34Clies between 34 and 43Dlies between 29 and 48 - Question 2 - Select One
The average salary of A, B and C is ₹10000and average expenditure of A , B and C is ₹6000 then the average saving of A , B and C:
A₹5500B₹4500C₹4000DCan't determined - Question 3 - Select One
As per data in the table, what is the percentage of students who got 20 or more marks
 A42B54C14D58
A42B54C14D58
The average salary per year during period 2001-2006 is
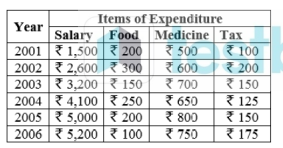 View Solution
View SolutionThere are three sections A, B and C in class X of a school. The average weight of all the students in classes A and B together is 26 kg. The average weight of all students in classes B and C together is 24 kg. What is the average weight of the students in all the three classes put together. If the average weight of the students in the classes A, B and C are 24 kg, 27 kg and 21 kg respectively.
View SolutionThe average marks obtained by 140 students in an examination is 90. If the average marks of passed students is 120 and the number of students who failed the examination are 90, then what is the average marks of students who failed the examination?
View SolutionThe average salary of managers is x and the average salary of workers is y. The number of the managers is 15 times of the number of workers. What is average salary of managers and workers together?
View SolutionThe average income of A, B and C is Rs. 12,000 per month and the average income of B, C and D is Rs. 15,000 per month. If the average salary of D be twice that of A, then the average salary of B and C is (in Rs.) :
View Solution

