In the above (i.e.., previous) problem, what is the ratio of P’s final amount to that of Q, if P and Q invest the same amounts??
(1.06)6
136100×(100106)6
100136×(106100)6
none of these
The correct Answer is:B
To find the ratio of P's final amount to that of Q's when both invest the same amount, we can follow these steps:
Step 1: Define the Investment Amount
Let the amount invested by both P and Q be x.
Step 2: Calculate P's Final Amount
P invests under Simple Interest (SI). The formula for the final amount A in SI is given by:
A=P+SI
Where SI=P⋅r⋅t100.
Here, P=x, r=6%, and t=6 years.
Calculating the Simple Interest for P:
SI=x⋅6⋅6100=36x100=36100x
Thus, the final amount for P is:
AP=x+36100x=x(1+36100)=x⋅136100
Step 3: Calculate Q's Final Amount
Q invests under Compound Interest (CI). The formula for the final amount A in CI is given by:
A=P(1+r100)t
Using the same values as before:
AQ=x(1+6100)6=x(106100)6
Step 4: Find the Ratio of P's Final Amount to Q's Final Amount
Now we need to find the ratio APAQ:
APAQ=x⋅136100x(106100)6
The x cancels out:
APAQ=136100(106100)6
Step 5: Simplify the Ratio
This can be simplified further:
APAQ=136100⋅(100106)6=136⋅1006100⋅1066=136⋅10051066
Final Answer
Thus, the ratio of P's final amount to Q's final amount is:
136⋅10051066
Let the amount invested by both P and Q be x.
P invests under Simple Interest (SI). The formula for the final amount A in SI is given by:
A=P+SI
Where SI=P⋅r⋅t100.
Here, P=x, r=6%, and t=6 years.
SI=x⋅6⋅6100=36x100=36100x
Thus, the final amount for P is:
AP=x+36100x=x(1+36100)=x⋅136100
Q invests under Compound Interest (CI). The formula for the final amount A in CI is given by:
A=P(1+r100)t
Using the same values as before:
AQ=x(1+6100)6=x(106100)6
Now we need to find the ratio APAQ:
APAQ=x⋅136100x(106100)6
The x cancels out:
APAQ=136100(106100)6
This can be simplified further:
APAQ=136100⋅(100106)6=136⋅1006100⋅1066=136⋅10051066
Thus, the ratio of P's final amount to Q's final amount is:
136⋅10051066
Topper's Solved these Questions
Similar Questions
Two friends P and Q started a business investing in the ratio of 5 6. R joined them after six months investing an amount equal to that of Q's. At the end of the year, 20% profit was earned which was equal to Rs. 98,000. What was the amount invested by R? Rs.105000 b. Rs.175000 c. Rs.210000 d. Data inadequate e. none of these
View SolutionIf P is the husband of Q and R is the mother of S and Q, what is R to P?
View Solution
Knowledge Check
In the previous problem
A2250B2600C1350Dcan't be determinedIn the previous problem if A gets a profit of Rs. 4200 the amount invested by B is :
A2250B2600C1350Dcan't be determined.
In above reaction P and Q areA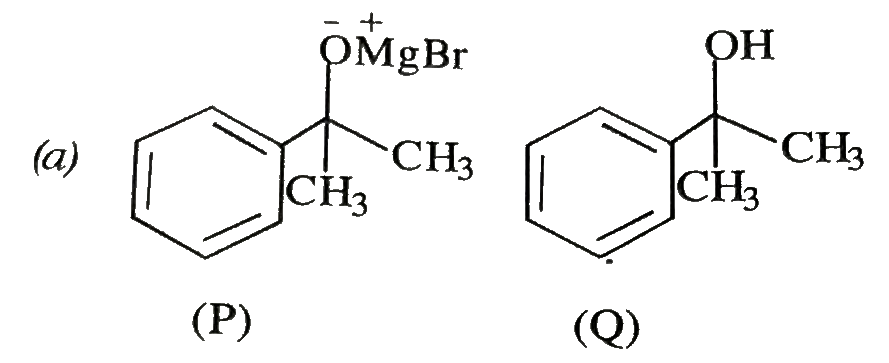 B
B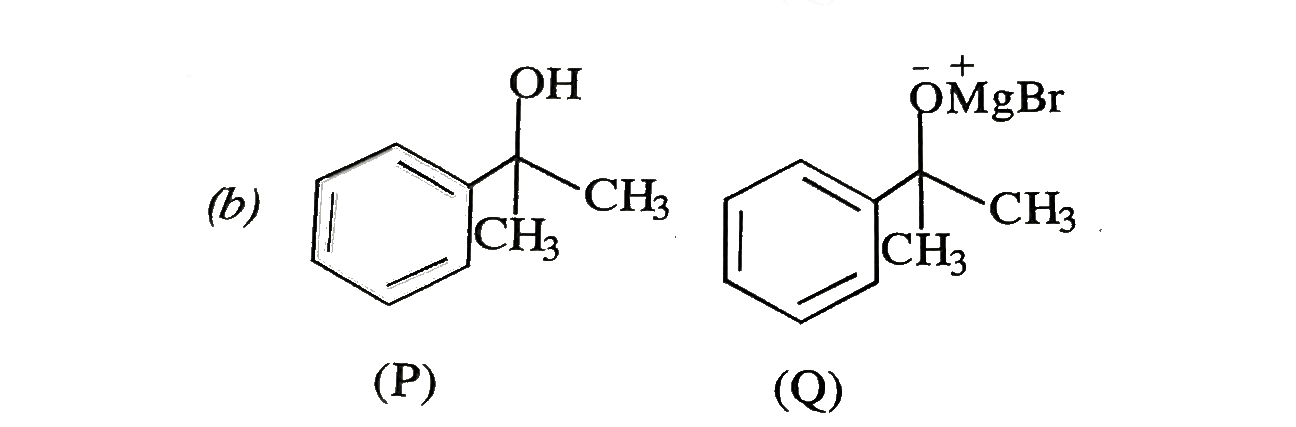 C
C D
D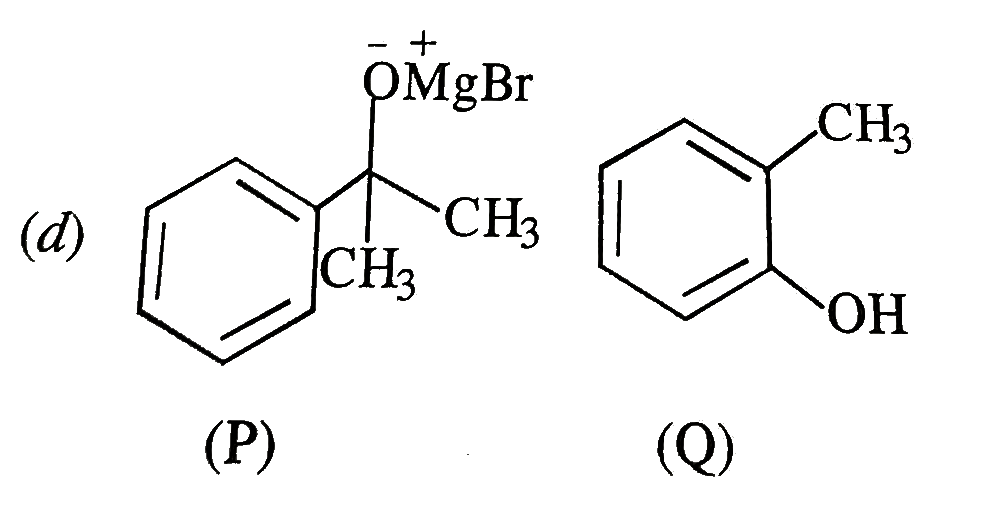
Two friends P and Q started a business investing in the ratio of 5:6. R joined them after six months investing an amount equal to that of Q's. At the end of the year, 20% profit was earned which was equal to Rs. 98,000 What was the amount invested by R?
View SolutionTwo persons P and Q lent certain amounts at the rate of interest for 2 years and 3 years, respectively, under compound interest. If their final amounts are in the ratio of 3:5, Q's amount at the end of the first year being Rs 8500 and P earned an interest of Rs 510 for the first year, then find the ratio of their principals.
View SolutionThe ratio of the speed of P, Q and R is 10:12:15 respectively. What is the ratio of the time taken by P. Q and R respectively to cover the same distance?
View SolutionThe ratio of the speed of P, Q and R is 10:12:15 respectively. What is the ratio of the time taken by P. Q and R respectively to cover the same distance?
View SolutionA sphere P of mass m moving with velocity u collides head on with another sphere Q of mass m which is at rest . The ratio of final velocity of Q to initial velocity of P is
( e = coefficient of restitution )
View Solution