The viscosity of mercury decreases with the rise in temperature (Table 21.1a). Check whether relation (34.10) is valid for mercury. Calculate the activation energy.

लिखित उत्तर

Verified by Experts

To check the exponential dependence of viscosity on temperature, find the dependence of the logarithm of viscosity on the reciprocal of the temperature. To do this, compile a new table (Table 21.1b) using the data of Table 21.1a. Using the data of the new table, plot

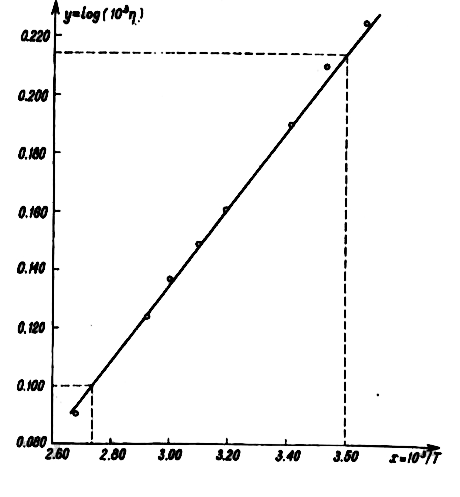
a graph on millimetre graph paper (Fig. 21.1). Almost all the points are seen to fall on the straight line
$y = a + b x, or log (10^{8} η) = a + 10^{0} + \frac{b}{T} = a + \frac{B}{T}$

Taking antilogarrithms we obtain
$10^{3} η = A \times 10^{B / T}$
the distinction from formula (34.10) being only in numerical coefficients.
To find the activation energy e, use two points lying on the straight line:
$x_{1} = 2.75, y_{1} = 0.100 and x_{2} = 3.60, y_{2} = 0.213$
The temperatures corresponding to these points are $T_{1} = 10^{3} / x_{1} = 364 K and T_{2} = 10^{3} / x_{2} = 278 K$ and the corresponding visocsities
are $η_{1} = 10^{- 3} \times 10 y_{1} = 1.26 \times 10^{- 3}$ Pa, * s and $η_{2} = 1.63 \times 10^{- 3} P a \cdot s$ .
The ratio or the viscosities is
$η_{2} : η_{1} = e_{0}^{ε_{0} / k T_{e}}, ε_{0}^{ε_{0} / h T_{1}} = exp {\frac{ε_{0} (T_{1} - T_{2})}{k T_{1} T_{2}}}$
Hence we obtain after taking the logarithms
$\frac{ε_{0} (T_{1} - T_{2})}{k T_{1} T_{2}} = \frac{ln (η_{2})}{η_{1}}$
or $ε_{0} = \frac{k T_{1} T_{2} ln (η_{2} / η_{1})}{T_{1} - T_{2}} - \frac{2.3 k T_{1} T_{2} log (η_{2} / η_{1})}{T_{1} - T_{2}}$

Updated on:21/07/2023