The coordinates of the three corners of a shaded face on a cubic unit cell are (12,12,1),(0,1,12) and (1,1,12) as shown below in the figure. Determine the Miller indices of the plane.

The intercepts of the shaded plane with the axes are ∞,2b and 2c respectively.

Thus, the Miller indices are (0 1 1).
Topper's Solved these Questions
- BOOK - RC MUKHERJEECHAPTER - SOLID AND LIQUID STATES EXERCISE - PROBLMES (ANSWERS BRACKTED WITH QUESTIONS)38videos
SOLID AND LIQUID STATES
- BOOK - RC MUKHERJEECHAPTER - SOLID AND LIQUID STATES EXERCISE - OBJECTIVE PROBLEMS51videos
SOLID AND LIQUID STATES
- BOOK - RC MUKHERJEECHAPTER - PROPERTIES OF GASESEXERCISE - OBJECTIVE PROBLEMS5videos
PROPERTIES OF GASES
- BOOK - RC MUKHERJEECHAPTER - VOLUMETRIC CALCULATIONS EXERCISE - OBJECTIVE PROBLEMS37videos
VOLUMETRIC CALCULATIONS
Similar Questions
The coordinate of the three corners of a shaded face on a cubic unit cell are (12,12,1),(0,1,12)and(1,1,12) as shown in the figure. Determine the Miller indices of the plane.
View SolutionThree vertices of a parallelogram are (1, 2, 1), (2, 5, 6) and (1, 6, 0) Find the coordinates of
the fourth vertex.View Solution
Knowledge Check
- Question 1 - Select One
Equation of plane passing through (1,1,0), (-2,2,-1) and (1,2,1) is
A2x+3y + 3z=5B2x-3y + 3z=5C2x + 3y - 3z+5=0D2x+3y - 3z=5
Three vertices of a parallelogram are (1, 2, 1), (2, 5, 6) and (1, 6, 0) Find the coordinates of
the fourth vertex.View SolutionDirection ratios of the normal to the plane passing through the point (0,1,1),(1,1,2)and(−1,2,−2) are
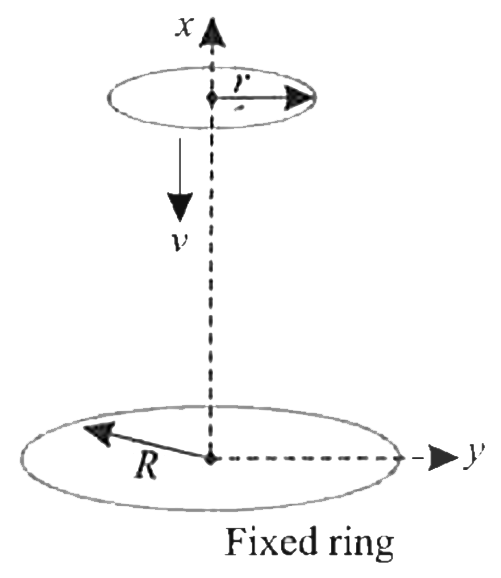
View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
 View Solution
View SolutionFind a unit vector normal to the plane through the points (1,1,1),(−1,2,3)and(2,−1,3).
View SolutionFind a unit vector normal to the plane through the points (1,1,1),(−1,2,3)and(2,−1,3).
View SolutionFind the vector equation of the plane passing through the points (1,1,0),(1,2,1)and(−2,2,−1).
View SolutionThe volume of tetrahedron whose vertices are (2,1,1),(1,-1,2),(0,1,-1) and (1,-2-1) is ........ (in cu.Units)
View Solution

