The tallest trees known are the redwoods in California. Assuming the height of a redwood to be 105 m, estimate the osmotic pressure required to push water up from the roots to the treetop
Topper's Solved these Questions
Similar Questions
Assuming the xylem tissues through which water rises from root to the branches in a tree to be of uniform cross-section find the maximum radius of xylem tube in a 10m high coconut tree so that water can rise to the top.
(Surface tension of water=0.1Nm, Angle of contact of water with xylem tube=60∘)
View SolutionWater leaks out from an open tank through a hole of area 2mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tankis 0.4m2. The pressure at the open surface and the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. a. Find the initial speed of water coming out of the hole. b. Findteh speed of water coming out when half of water has leaked out. c. Find the volume of water leaked out during a time interval dt after the height remained is h. Thus find the decrease in height dh in term of h and dt.
d. From the result of part c. find the time required for half of the water to leak out.
View Solution
Knowledge Check
Assuming the xylem tissues through which water rises from root to the branches in a tree to be of uniform cross-section find the maximum radius of xylem tube in a 10m high coconut tree so that water can rise to the top.
(Surface tension of water=0.1Nm, Angle of contact of water with xylem tube=60∘)A1cmB1mmC10μmD1μmWhen liquid medicine ρ is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop froms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is osperical becaus ethat requires a minimum increase in its surface energy. To datermine the size., we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force become smaller than the wight of the drop, the drop gets detached from the droppr.
A glass capillary tube is of the shape of a truncated cone with an apex angle α so that its two ends have cross sections of different raddi. When dipped in water verically, water rises in it to a height h, where the radius of its cross section is b. If the surface tension of water is S, its density is ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)
 A2Sbρgcos(θ−α)B2Sbρgcos(θ+α)C2Sbρgcos(θ−α/2)D2Sbρgcos(θ+α/2)
A2Sbρgcos(θ−α)B2Sbρgcos(θ+α)C2Sbρgcos(θ−α/2)D2Sbρgcos(θ+α/2)A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]A6B4C2D8
A cylindrical container has cross sectional area of A=0.05m2 and length L = 0.775 m. Thickness of the wall of the container as well as mass of the container is negligible. The container is pushed into a water tank with its open end down. It is held in a position where its closed end is h = 5.0 m below the water surface. What force is required to hold the container in this position? Assume temperature of air to remain constant.
Atmospheric pressure P0=1x×105 Pa, Acceleration due to gravity g=10m/s2
Density of water = 103kg/m3
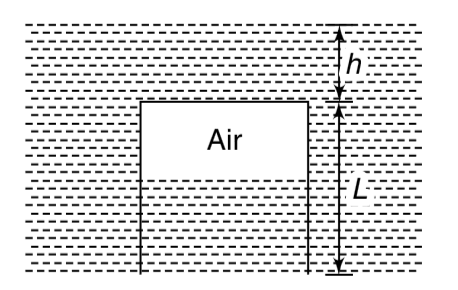
View SolutionA lake filled with water has depth H, A pipe of length slightly less than H lies at the bottom of the lake. It contains an ideal gas filled up to a length of H10 A smooth an ideal gas filled up to a length gas in place. Now the pipe is slowly raised to vertical position (see figure). Assume that temperature of the gas remains Constant and neglect the atmospheric pressure.
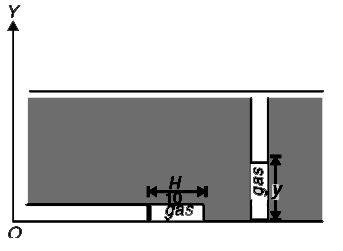
(a) Plot the variation of pressure inside the lake as a function of height y from the base. Let the height of piston frm the base, after the pipe is made vertical, by y. plot the variation of gas pressure as a function of y in the first graph itself.
(b) In equilibrium the gas pressure and the pressure due to water on the piston must be equal. Using this solve for equilibrium height y0 of the piston. You get two answers. Which one is correct and why?
View SolutionSubmarine rescue. When the U.S. submarine Squalus became disabled at a depth of 80 m, a cylindrical chamber was lowered from a ship to rescue the crew. The chamber had a radius of 1.00 m and a height of 3.50 m, was open at the bottom, and held two rescuers. It slid along a guide cable that a diver had attached to a hatch on the submarine. Once the chamber reached the hatch and clamped to the hull, the crew could escape into the chamber. During the descent, air was released from tanks to prevent water from flooding the chamber. Assume that the interior air pressure matched the water pressure at depth h as given by P0+ρgh, where P0 = 1.000 atm is the surface pressure and p= 1024 kg/m3 is the density of seawater. Assume a surface temperature of 20.0°C and a submerged water temperature of −40.0∘C. (a) What is the air volume in the chamber at the surface? (b) If air had not been released from the tanks, what would have been the air volume in the chamber at depth h = 80.0 m? (c) How many moles of air were needed to be released to maintain the original air volume in the chamber?
View SolutionA cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]
View SolutionA cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]
View Solution
