State Hardy Weinberg's principle.
Step-by-Step Solution:
1. Definition of Hardy-Weinberg Principle: The Hardy-Weinberg principle states that the genotypic and allelic frequencies in a population will remain constant from generation to generation in the absence of evolutionary influences.
2. Conditions for Hardy-Weinberg Equilibrium: For the Hardy-Weinberg principle to hold true, certain assumptions must be met:
- No Mutation: There should be no changes in the DNA sequence that would introduce new alleles into the population.
- Random Mating: Individuals in the population must mate randomly, meaning that mate selection is not influenced by genotype or phenotype.
- No Gene Flow: There should be no migration of individuals into or out of the population, which could introduce new alleles or remove existing ones.
- Large Population Size: The population must be large enough to prevent random fluctuations in allele frequencies (genetic drift).
- No Natural Selection: All individuals must have equal chances of survival and reproduction, meaning that no particular genotype is favored over another.
3. Mathematical Representation: The Hardy-Weinberg principle can be represented mathematically using the equation:
- p2+2pq+q2=1
- Where:
- p = frequency of the dominant allele
- q = frequency of the recessive allele
- p2 = frequency of homozygous dominant genotype
- q2 = frequency of homozygous recessive genotype
- 2pq = frequency of heterozygous genotype
4. Conclusion: The Hardy-Weinberg principle is a foundational concept in population genetics, providing a baseline expectation for the genetic structure of a population under ideal conditions.
- No Mutation: There should be no changes in the DNA sequence that would introduce new alleles into the population.
- Random Mating: Individuals in the population must mate randomly, meaning that mate selection is not influenced by genotype or phenotype.
- No Gene Flow: There should be no migration of individuals into or out of the population, which could introduce new alleles or remove existing ones.
- Large Population Size: The population must be large enough to prevent random fluctuations in allele frequencies (genetic drift).
- No Natural Selection: All individuals must have equal chances of survival and reproduction, meaning that no particular genotype is favored over another.
- p2+2pq+q2=1
- Where:
- p = frequency of the dominant allele
- q = frequency of the recessive allele
- p2 = frequency of homozygous dominant genotype
- q2 = frequency of homozygous recessive genotype
- 2pq = frequency of heterozygous genotype
Topper's Solved these Questions
- EVOLUTIONBOOK - ICSECHAPTER - EVOLUTIONEXERCISE - PREVIOUS YEAR.S BOARD PAPER QUESTIONS (Short Answer Type-l Questions)
4 Videos
- EVOLUTIONBOOK - ICSECHAPTER - EVOLUTIONEXERCISE - PREVIOUS YEAR.S BOARD PAPER QUESTIONS (Short Answer Type-lI Questions)
10 Videos
- EVOLUTIONBOOK - ICSECHAPTER - EVOLUTIONEXERCISE - PRACTICE QUESTIONS (Long Answer Type Questions)
26 Videos
- ENVIRONMENTAL ISSUESBOOK - ICSECHAPTER - ENVIRONMENTAL ISSUESEXERCISE - COMPETITION CORNER (ASSERTION AND REASON TYPE QUESTIONS (FOR AIIMS ASPIRANTS))
9 Videos
- HUMAN HEALTH AND DISEASE BOOK - ICSECHAPTER - HUMAN HEALTH AND DISEASE EXERCISE - COMPETITION CORNER (OBJECTIVE TYPE QUESTIONS) (Assertion and Reason Type Questions (For AIIMS aspirants))
28 Videos
Similar Questions
Knowledge Check
The Hardy-Weinberg principle cannot operate if
APopulation is largeBFree interbreeding among all membersCFrequent mutations occur in populationDPopulation does not interact with other population
Choose the WRONG statement regarding the Hardy - Weinberg principle.
View SolutionIf p2+2pq+q2=1. Explain this algebraic equation on the basis of Hardy Weinberg's principle.
View Solution(a ) Write the Hardy-Weinberg principle.
(b) Explain the three different ways in which natural selection can affect the frequency of a heritable trait in a population shown in the graph given below.
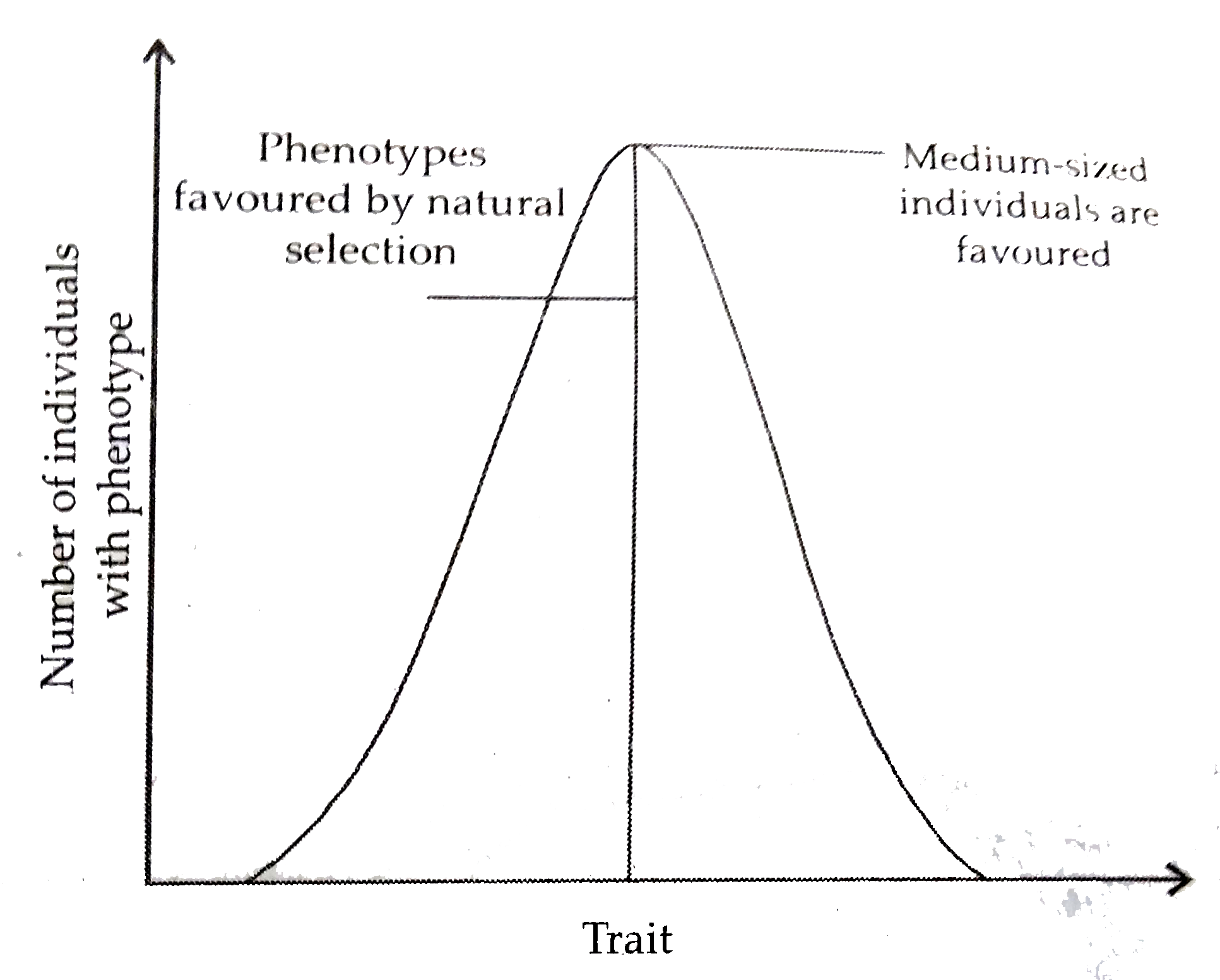
View Solution(a ) Write the Hardy-Weinberg principle.
(b) Explain the three different ways in which natural selection can affect the frequency of a heritable trait in a population shown in the graph given below.

View SolutionAccording to Hardy-Weinberg's principle, if allele one is denoted as 'A' and allele two as 'a' and their frequencies are denoted by p and q, and if random mating occurs. The frequency of heterozygous individual would be :
View SolutionAccording to the Hardy-Weinberg principle, the allele frequency of a population remains costant. How do you interpret the change of frequency of alleles in a population ?
View SolutionAccording to Hardy-Weinberg principle, sum total of all the allellic frequencies is
View Solution
