The value of is (i) positive (ii) negative (iii) 0 (iv) cannot be determined
positive
negative
0
cannot be determined
The correct Answer is:D
To solve the problem of finding the value of the expression 1+i+i2+…+in, we can follow these steps:
Step 1: Understand the powers of i
The powers of i (where i=√−1) cycle every four terms:
- i0=1
- i1=i
- i2=−1
- i3=−i
- i4=1 (and the cycle repeats)
Step 2: Write the sum explicitly
We can express the sum as:
S=1+i+i2+i3+i4+…+in
Step 3: Determine the number of complete cycles
Since the powers of i repeat every four terms, we can determine how many complete cycles of four fit into n:
- Let k=⌊n4⌋ (the number of complete cycles)
- Let r=nmod4 (the remainder when n is divided by 4)
Step 4: Calculate the sum based on r
The sum can be broken down into complete cycles and the remaining terms:
S=k⋅(1+i+(−1)+(−i))+(remaining terms)
Since 1+i−1−i=0, the contribution from complete cycles is 0.
Now, we need to add the remaining terms based on the value of r:
- If r=0: S=0
- If r=1: S=1
- If r=2: S=1+i
- If r=3: S=1+i−1−i=0
Step 5: Conclusion
The value of S depends on n:
- If n≡0mod4 or n≡3mod4, then S=0.
- If n≡1mod4, then S=1 (positive).
- If n≡2mod4, then S=1+i (which has a real part of 1, hence positive).
Since the value of S depends on n, we conclude that the value of 1+i+i2+…+in cannot be determined without knowing n.
Final Answer
The correct option is (iv) cannot be determined.
The powers of i (where i=√−1) cycle every four terms:
- i0=1
- i1=i
- i2=−1
- i3=−i
- i4=1 (and the cycle repeats)
We can express the sum as:
S=1+i+i2+i3+i4+…+in
Since the powers of i repeat every four terms, we can determine how many complete cycles of four fit into n:
- Let k=⌊n4⌋ (the number of complete cycles)
- Let r=nmod4 (the remainder when n is divided by 4)
The sum can be broken down into complete cycles and the remaining terms:
S=k⋅(1+i+(−1)+(−i))+(remaining terms)
Since 1+i−1−i=0, the contribution from complete cycles is 0.
- If r=0: S=0
- If r=1: S=1
- If r=2: S=1+i
- If r=3: S=1+i−1−i=0
The value of S depends on n:
- If n≡0mod4 or n≡3mod4, then S=0.
- If n≡1mod4, then S=1 (positive).
- If n≡2mod4, then S=1+i (which has a real part of 1, hence positive).
The correct option is (iv) cannot be determined.
Topper's Solved these Questions
Similar Questions
The position-time (x-t) graph of an object in uniform motion is shown below, the velocity of object is
(i) Positive
(ii) Negative
(iii) Zero
(iv) None of these
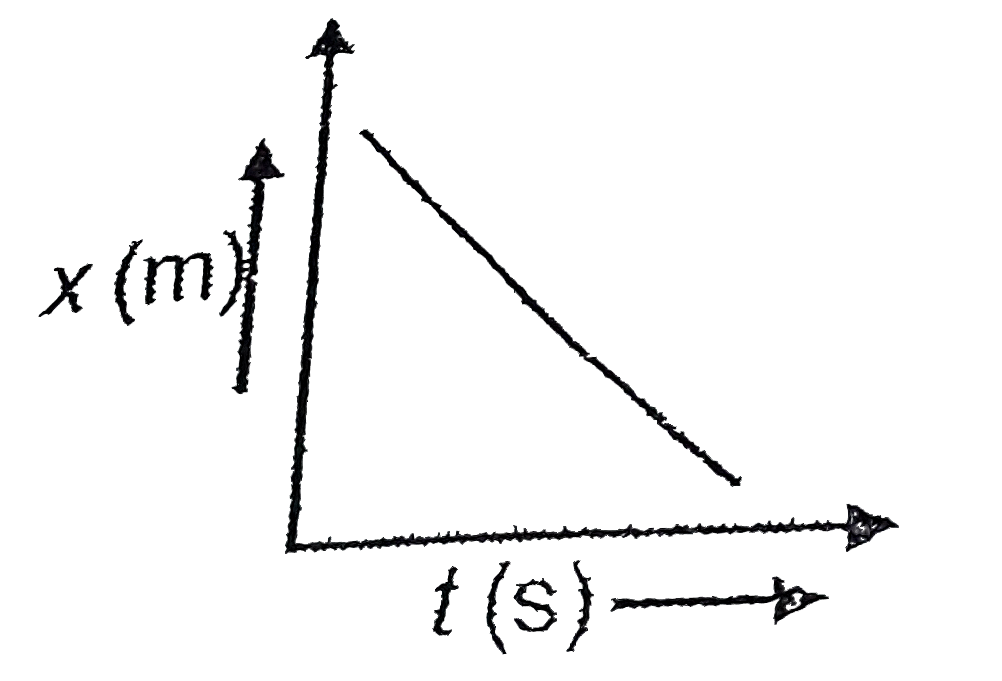 View Solution
View SolutionIf the velocity of an object is increasing and changing at a uniform rate then the acceleration of the object is
(i) Positive (ii) Zero
(iii) Negative (iv) Not definedView Solution
Knowledge Check
- Question 1 - Select One
The argument of -I is: (i) π (ii) −π (iii) −π2 (iv) π2
AπB−πC−π2Dπ2 - Question 2 - Select One
The value of sin(45∘+θ)−cos(45∘−θ) is
A2cosθB0C2sinθD1 - Question 3 - Select One
The argument of 1+i1−i is (i) 0 (ii) −π2 (iii) π2 (iv) π
A0B−π2Cπ2Dπ
Find the values of the following :
(i) i73
(ii) i−6
(iii) 1iView SolutionWhich of the following statements are true? (i) The sum of a number and its opposite is zero. (ii) The sum of two negative integers is a positive integer. (iii) The sum of a negative integer and a positive integer is always a negative integer. (iv) The successor of −1 is 1. (v) The sum of three different integers can never be zero.
View SolutionFor all n∈N,2n+1+32n−1 is divisible by:
(i) 5
(ii) 7
(iii) 14
(iv) 135View SolutionIf (1+i1−i)x=1∀n∈N is (i) x = 2n+1 (ii) x =4n (iii) x=2n (iv) x=4n+1
View SolutionLtx→0|x|x is equal to (i) 1 (ii) −1 (iii) 0 (iv) does not exist
View Solution

