Can two numbers have 12 as their H.C.F. and 234 as their L.C.M? Give reason to justify your answer.
To determine whether two numbers can have 12 as their H.C.F. (Highest Common Factor) and 234 as their L.C.M. (Lowest Common Multiple), we can follow these steps:
Step 1: Understand the relationship between HCF and LCM
The relationship between the HCF and LCM of two numbers a and b is given by the formula:
HCF×LCM=a×b
This means that the product of the HCF and LCM of two numbers is equal to the product of the numbers themselves.
Step 2: Represent the two numbers
Since the HCF of the two numbers is 12, we can express the two numbers as:
a=12xandb=12y
where x and y are co-prime integers (they have no common factors other than 1).
Step 3: Calculate the LCM using the representation
The LCM of the two numbers a and b can be calculated as:
LCM(a,b)=a×bHCF(a,b)=(12x)×(12y)12=12xy
Step 4: Set the LCM equal to 234
According to the problem, the LCM is given as 234. Therefore, we set up the equation:
12xy=234
Step 5: Solve for xy
To find xy, we divide both sides of the equation by 12:
xy=23412=19.5
Step 6: Analyze the result
Since x and y are integers, their product xy must also be an integer. However, 19.5 is not an integer, which means that there are no integer values for x and y that satisfy this equation.
Conclusion
Since we cannot find integer values for x and y such that their product equals 19.5, it is not possible for two numbers to have 12 as their H.C.F. and 234 as their L.C.M.
Final Answer
No, two numbers cannot have 12 as their H.C.F. and 234 as their L.C.M. because it leads to a non-integer product for x and y.
---
The relationship between the HCF and LCM of two numbers a and b is given by the formula:
HCF×LCM=a×b
This means that the product of the HCF and LCM of two numbers is equal to the product of the numbers themselves.
Since the HCF of the two numbers is 12, we can express the two numbers as:
a=12xandb=12y
where x and y are co-prime integers (they have no common factors other than 1).
The LCM of the two numbers a and b can be calculated as:
LCM(a,b)=a×bHCF(a,b)=(12x)×(12y)12=12xy
According to the problem, the LCM is given as 234. Therefore, we set up the equation:
12xy=234
To find xy, we divide both sides of the equation by 12:
xy=23412=19.5
Since x and y are integers, their product xy must also be an integer. However, 19.5 is not an integer, which means that there are no integer values for x and y that satisfy this equation.
Since we cannot find integer values for x and y such that their product equals 19.5, it is not possible for two numbers to have 12 as their H.C.F. and 234 as their L.C.M.
No, two numbers cannot have 12 as their H.C.F. and 234 as their L.C.M. because it leads to a non-integer product for x and y.
Similar Questions
Can two numbers have 15 as their H.C.F. and 110 as their L.C.M.? Give reason to justify your answer.
View SolutionCan two numbers have 18 as their HCF and 380 as their LCM? Give reason.
View SolutionCan two numbers have 18 as their HCF and 146 as their LCM? Give reasons.
View SolutionCan two number have 18 as their HCF and 380 as their LCM? Give reason
View SolutionTwo numbers have 12 as their HCF and 350 as their LCM (True/false).
View SolutionCan two numbers have 12 as their HCF and 512 as their LCM? Justify your answer.
View SolutionCan two numbers has 16 as H.C.F. and 380 as L.C.M .
View SolutionConsider the following circuit :
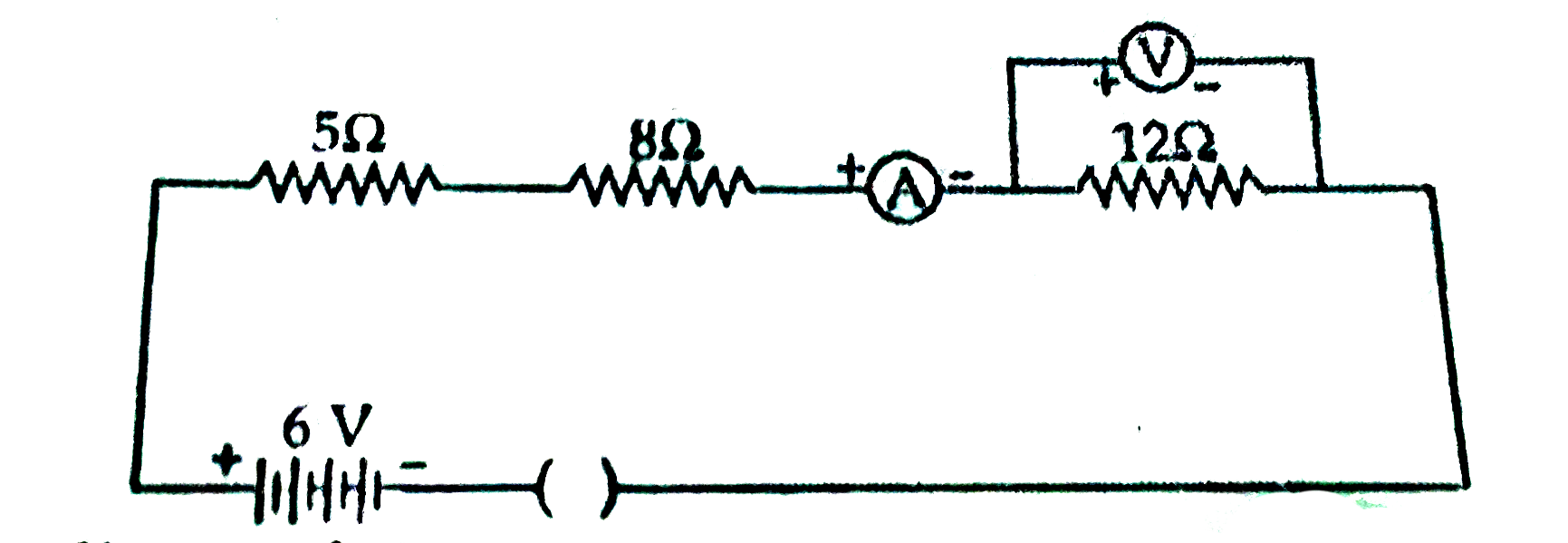
What would be the readings of the ammeter and the voltmeter when key is closed ? Give reason to justify your answers .
View SolutionA gas cylinder can hold 1 kg of hydrogen gas at room temperature and 1 atm pressure. Calculate the following:
The number of molecules of carbon dioxide in the cylinder. Give reasons to justify your answer. Mass of the substance
View SolutionAnswer the following:
(i) Obtain the expression for the cyclotron frequency.
(ii) A deuteron and a proton are accelerated by the cyclotron. Can both be accelerated with the same oscillator frequency ? Give reason to justify your answer.
View Solution