From the adjoining figure , write?
all pairs of parallel lines
(ii) all pairs of intersecting lines.
(iii) lines whose point of intersection is E.
(iv) one set of three- non collinear points.
(v) all sets of collinear points.

Step by step video & image solution for From the adjoining figure , write? all pairs of parallel lines (ii) all pairs of intersecting lines. (iii) lines whose point of intersection is E. (iv) one set of three- non collinear points. (v) all sets of collinear points. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Similar Questions
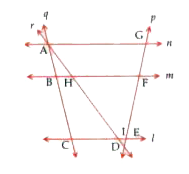
In the adjoining figure write.
(i) all pairs of parallel lines
(ii) all pairs of intersecting lines.
(iii) Concurrent lines.
(iv) Collinear points.
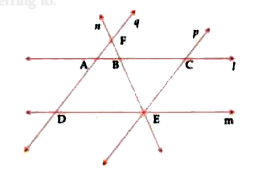
View SolutionFrom the given figure, write
(i) all pairs of parallel lines
(ii) all pairs of intersecting lines
(iii) concurrent lines and point of concurrence
(iv) collinear points
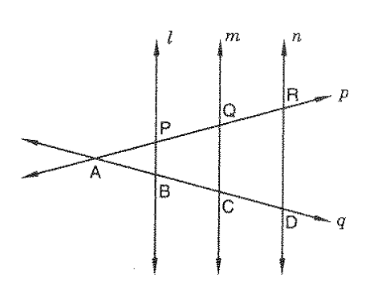
View SolutionFrom Figure, name
(i)All pairs of parallel lines.
(ii)all pairs of intersecting lines.
(iii)ines of whose point of intersection in P
(iv)lines whose point of intersection in C
(v)lines whose point of intersection in R
(vi)Collinear points.
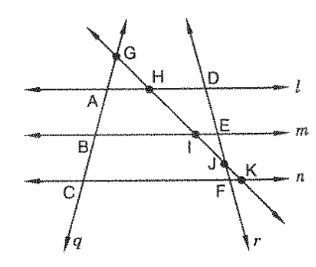
View SolutionForm Fig., write
(i)all pairs of parallel lines. (ii)all pairs of intersection lines. (iii)lines whose point of intersection is l . (iv) lines whose point of intersection is D . (v) lines whose point of intersection is E . (vi) lines whose point of intersection is A .
View SolutionIn the adjoining figure
(a) Name
(i) Parallel lines
(ii) all pairs of intersecting lines.
(iii) concurrent lines.
( b) State whether true of false.
(i) points A,B and D are collinear.
(ii) lines AB and ED intersects at C .
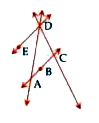
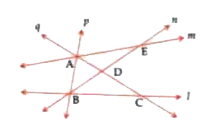
View SolutionFrom the adjoining figure , write?
(i) Collinear points
(ii) Concurrent lines and their point of concurrence.
View SolutionConsider the given figure write down the sets of collinear points.

View SolutionHow many lines can be drawn through there:
non -collinear points ?
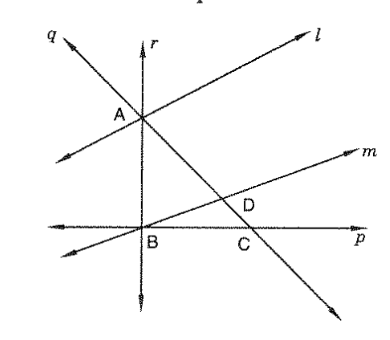
View SolutionFrom Figure, write
(i)Lines intersecting at A
(ii)Lines intersecting at B
(iii)Concurrent lines and their point of concurrence.
View SolutionThe point of intersection of lines is (α,β) , then the equation whose roots are α,β, is
View Solution
