Two vessels A and B contains acid of different concentration. The capacity of A and B are 6 lt and 3 lt respectively. We take out same quantity from both vessels and put into one another, now the concentration in both vessel are same. Find the taken out quantity.
2 litres
1 litres
112 litres
34 litres
The correct Answer is:A
To solve the problem step by step, we will denote the quantity taken out from each vessel as x liters.
Step 1: Define the concentrations before the exchange
- Let the concentration of acid in vessel A be CA and in vessel B be CB.
- The capacity of vessel A is 6 liters, and the capacity of vessel B is 3 liters.
Step 2: Assume the initial concentrations
- Assume vessel A contains a certain concentration of acid, say CA=a6, where a is the amount of acid in vessel A.
- Assume vessel B contains CB=b3, where b=0 since it contains only water (0% acid).
Step 3: After taking out x liters from both vessels
- From vessel A, after taking out x liters, the amount of acid left is a−a6⋅x and the total volume is 6−x.
- From vessel B, after taking out x liters, the amount of acid is b3⋅x and the total volume is 3−x.
Step 4: Set up the equation for equal concentrations
After exchanging x liters, the concentration in both vessels becomes equal:
(a−a6⋅x)(6−x)=(0+0)(3−x)
Since vessel B initially had no acid, the concentration in vessel B after adding x liters from vessel A will be:
a6⋅x3
Step 5: Cross-multiply to solve for x
Cross-multiplying gives:
(a−a6⋅x)⋅3=(0+0)⋅(6−x)
This simplifies to:
3a−3a6⋅x=0
Rearranging gives:
3a=3a6⋅x
Thus:
x=2 liters
Conclusion
The quantity taken out from each vessel is 2 liters.
- Let the concentration of acid in vessel A be CA and in vessel B be CB.
- The capacity of vessel A is 6 liters, and the capacity of vessel B is 3 liters.
- Assume vessel A contains a certain concentration of acid, say CA=a6, where a is the amount of acid in vessel A.
- Assume vessel B contains CB=b3, where b=0 since it contains only water (0% acid).
- From vessel A, after taking out x liters, the amount of acid left is a−a6⋅x and the total volume is 6−x.
- From vessel B, after taking out x liters, the amount of acid is b3⋅x and the total volume is 3−x.
After exchanging x liters, the concentration in both vessels becomes equal:
(a−a6⋅x)(6−x)=(0+0)(3−x)
a6⋅x3
Cross-multiplying gives:
(a−a6⋅x)⋅3=(0+0)⋅(6−x)
This simplifies to:
3a−3a6⋅x=0
Rearranging gives:
3a=3a6⋅x
Thus:
x=2 liters
The quantity taken out from each vessel is 2 liters.
Topper's Solved these Questions
Similar Questions
There are two vessels containing 2 mixture of acid having different concentration. A contains 8 ltacid and B contains 6 ltacid. 2x ltwas taken out from vessel A and x ltof mixture was taken out from vessel B and are poured into each other and their concentation becomes equal. Find the value of x.
View SolutionTwo vessels contain spirit of 0.5and0.75 concentrations. If 2 lt from the first vessel and 3 lt from the second vessel are mixed, then what will be the ratio of the spirit and the water in the resultant solution?
View Solution
Knowledge Check
- Question 1 - Select One
Two vessels A and B contains acid and water in the ratio 4:3 and 5:3 respectively. Then the ratio in which these mixtures to be mixed to obtain a new mixture in vessel C containing acid and water in the ratio 3:2 is
A5:8B7:8C7:5D4:7 - Question 2 - Select One
Three vessels A, B and C of different shapes contain water upto the same height in the figure. PA,PBandPC be the pressure exerted by the water at the bottom of the vessels A, B and C respectively. Then
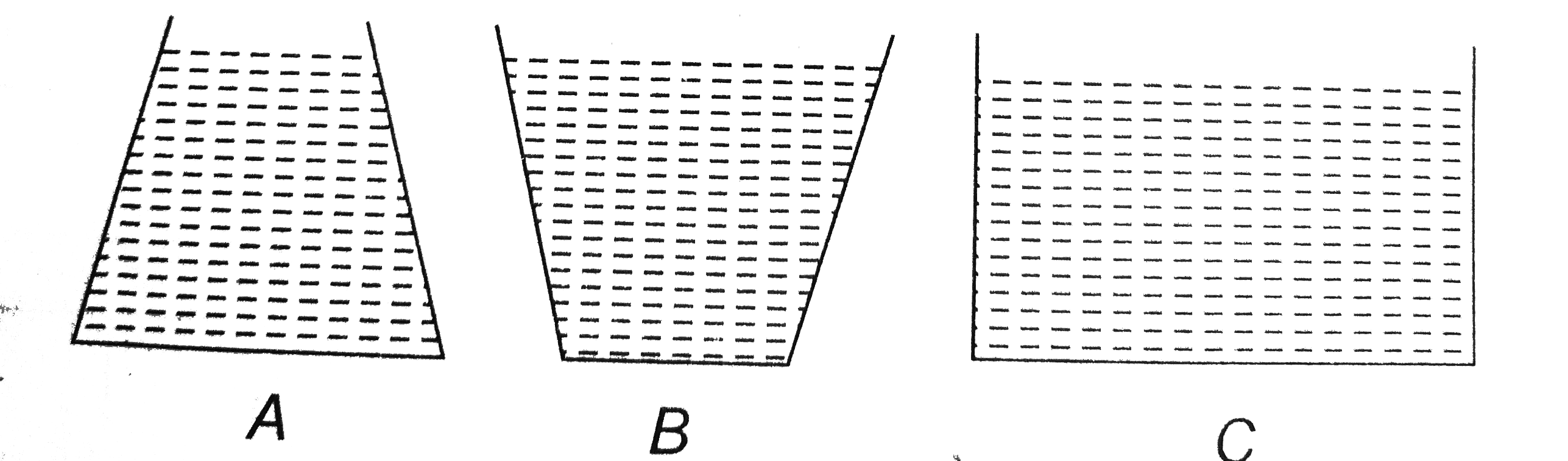 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC - Question 3 - Select One
Two vessels A and B contain spirit and water mixed in the ratio 5:2 and 7:6 respectively. Find the ratio in which these mixture be mixed to obtain a new mixture in vessel C containing spirit and water in the ratio 8:5?
Aa. 4:8Bb. 3:9Cc. 7:9Dd. 5:6
Two solutions of milk and water are kept in two vessels A and B. The ratio of quantity of milk in vessels A and B is 4 : 5 while the ratio of quantity of water in vessels A and B is 8 : 9. It is known that that the concentration of milk in one of these vessels between 60% and 80%. What could be the concentration of milk in the other vessel?
View SolutionTwo identical vessels A and B contain mixtures of milk and water in the ratios 4:5 and 5:1 respectively in what ratio should quantities of mixtures be taken from A and b to form a mixture in which milk to water is in the ratio 5:4?
View SolutionVessels A and B contain mixtures of milk and water in the ratios 4:5 and 5: 1 respectively. In what ratio should quantities of mixture be taken from A and B to form a mixture in which milk to water is in the ratio 5: 4?
View SolutionTwo vessels P and Q contain 'a' litres of petrol and 'b' litres of kerosene respectively. 'c' litres of petrol and same quantity of kerosene is taken out and then transferred to Q and P respectively. This process is repeated several times. If after the first operation the quantity of petrol or kerosene in either of P and Q does not change. What is the value of 'c'?
View SolutionThere are two vessels A and B containing 25 litres each of pure milk and pure water respectively. 5 litres of milk from A is taken and poured into B, then 6 litres of mixture from B is taken and poured in A. What is the ratio of water in A and B respectively :
View Solution

